题目内容
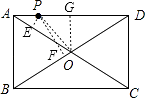
【题目】如图，点P是矩形ABCD的边AD上的一动点，AB=6，BC=8，则点P到矩形的两条对角线AC和BD的距离之和是（ ）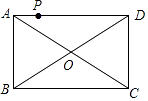
A.4.8
B.5
C.6
D.7.2
【答案】A
【解析】解：
如图，过P作PE⊥AC于点E，作PF⊥BD于点F，过O作OG⊥AD，连接OP，
∵四边形ABCD为矩形，
∴∠ABC=90°，
∵AB=6，BC=8，
∴AC=BD=10，
∴AO=OD=5，GO= 
AB=3，
∵S△AOD=S△AOP+S△DOP，
∴ ADGO= AOPE+ DOPF，
∴8×3=5PE+5PF，
∴PE+PF= 
=4.8，
即点P到到矩形的两条对角线AC和BD的距离之和是4.8，
所以答案是：A．
【考点精析】本题主要考查了矩形的性质的相关知识点，需要掌握矩形的四个角都是直角，矩形的对角线相等才能正确解答此题．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
【题目】某蒜薹生产基地喜获丰收，收获蒜薹200吨．经市场调查，可采用批发、零售、冷库储藏后销售三种方式，并按这三种方式销售，计划平均每吨的售价及成本如下表：
销售方式 | 批发 | 零售 | 储藏后销售 |
售价（元/吨） | 3000 | 4500 | 5500 |
成本（元/吨） | 700 | 1000 | 1200 |
若经过一段时间，蒜薹按计划全部售出获得的总利润为y（元），蒜薹零售x（吨），且零售量是批发量的 
．
（1）求y与x之间的函数关系式；
（2）由于受条件限制，经冷库储藏售出的蒜薹最多80吨，求该生产基地按计划全部售完蒜薹获得的最大利润．
