题目内容
【题目】如图,抛物线![]() 与
与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连结
,连结![]() ,点
,点![]() 在抛物线上,直线
在抛物线上,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值及直线
的值及直线![]() 的函数表达式;
的函数表达式;
(2)点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在
在![]() 轴正半轴上,连结
轴正半轴上,连结![]() 与直线
与直线![]() 交于点
交于点![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,若
,若![]() 为
为![]() 的中点.
的中点.
①求证:![]() ;
;
②设点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 的长(用含
的长(用含![]() 的代数式表示).
的代数式表示).
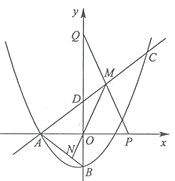
【答案】(1)c=-3; 直线AC的表达式为:y=![]() x+3;(2)①证明见解析;②
x+3;(2)①证明见解析;②![]()
【解析】
试题分析:(1)把点C(6,![]() )代入
)代入![]() 中可求出c的值;令y=0,可得A点坐标,从而可确定AC的解析式;
中可求出c的值;令y=0,可得A点坐标,从而可确定AC的解析式;
(2)①分别求出tan∠OAB=tan∠OAD=![]() ,得∠OAB=tan∠OAD,再由M就PQ的中点,得OM=MP,所以可证得∠APM=∠AON,即可证明
,得∠OAB=tan∠OAD,再由M就PQ的中点,得OM=MP,所以可证得∠APM=∠AON,即可证明![]() ;
;
②过M点作ME⊥x轴,垂足为E,分别用含有m的代数式表示出AE和AM的长,然后利用![]() 即可求解.
即可求解.
试题分析:(1)把点C(6,![]() )代入
)代入![]()
解得:c=-3
∴![]()
当y=0时,![]()
解得:x1=-4,x2=3
∴A(-4,0)
设直线AC的表达式为:y=kx+b(k≠0)
把A(-4,0),C(6,![]() )代入得
)代入得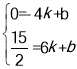
解得:k=![]() ,b=3
,b=3
∴直线AC的表达式为:y=![]() x+3
x+3
(2)①在RtΔAOB中,tan∠OAB=![]()
在RtΔAOD中,tan∠OAD=![]()
∴∠OAB=∠OAD
∵在RtΔPOQ中,M为PQ的中点
∴OM=MP
∴∠MOP=∠MPO
∵∠MPO=∠AON
∴∠APM=∠AON
∴ΔAPM∽ΔAON
②如图,过点M作ME⊥x轴于点E
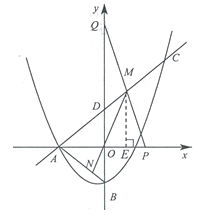
又∵OM=MP
∴OE=EP
∵点M横坐标为m
∴AE=m+4 AP=2m+4
∵tan∠OAD=![]()
∴cos∠EAM=cos∠OAD=![]()
∴AM=![]() AE=
AE=![]()
∵ΔAPM∽ΔAON
∴![]()
∴AN=![]()

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目