Question

【题目】在△ABC中，AB=10，AC=2 ，BC边上的高AD=6，则另一边BC等于 ．

Answer 1

【答案】10或6
【解析】解：根据题意画出图形，如图所示，

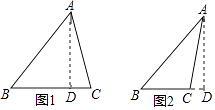
如图1所示，AB=10，AC=2 ，AD=6，

在Rt△ABD和Rt△ACD中，

根据勾股定理得：BD= =8，CD= =2，

此时BC=BD+CD=8+2=10；

如图2所示，AB=10，AC=2 ，AD=6，

在Rt△ABD和Rt△ACD中，

根据勾股定理得：BD= =8，CD= =2，

此时BC=BD﹣CD=8﹣2=6，

则BC的长为6或10．

所以答案是：10或6．

【考点精析】掌握勾股定理的概念是解答本题的根本，需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．