题目内容
【题目】(教材呈现)
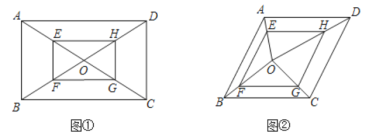
下图是华师版九年级上册数学教材第79页的部分内容.
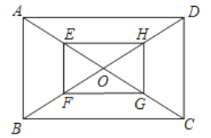
如图,矩形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 、
、![]() 的中点,求证:四边形
的中点,求证:四边形![]() 是矩形.
是矩形.
请根据教材内容,结合图①,写出完整的解题过程.
(结论应用)
(1)在图①中,若![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为__________;
的面积为__________;
(2)如图②,在菱形![]() 中,
中,![]() ,
,![]() 是其内任意一点,连接
是其内任意一点,连接![]() 与菱形
与菱形![]() 各顶点,四边形
各顶点,四边形![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 、
、![]() 上,
上,![]() ,
,![]() ,且
,且![]() ,若
,若![]() 与
与![]() 的面积和为
的面积和为![]() ,则菱形
,则菱形![]() 的周长为___________.
的周长为___________.
【答案】证明见解析;(1)![]() ;(2)24
;(2)24
【解析】
由矩形的性质得出OA=OC=OB=OD,再证出OE=OF=OG=OH,即可得出结论.
(1)证明△OEF为等边三角形,得出∠EFO=60°,可求出![]() ,则答案即可求出;
,则答案即可求出;
(2)过点G作GN⊥EF于点N,由条件可知四边形EFGH为平行四边形,可得∠EFG=60°,设![]() ,则
,则![]() ,由
,由![]() 与
与![]() 的面积和为
的面积和为![]() 可列出方程求出x,证明
可列出方程求出x,证明![]() ,可得
,可得![]() ,可求出AB的长,则答案可求出.
,可求出AB的长,则答案可求出.
解:∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,![]() 的中点为
的中点为![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∵![]() ,
,
∴四边形![]() 是矩形.
是矩形.
(1)解:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 的面积为
的面积为![]() ,
,
故答案为:![]() .
.
(2)过点![]() 作
作![]() 于点
于点![]() ,
,
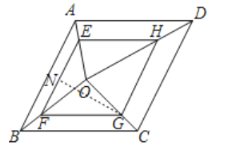
∵![]() ,且
,且![]()
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∵![]() 与
与![]() 的面积和为
的面积和为![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴菱形![]() 的周长为24.
的周长为24.
故答案为:24.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案【题目】小张同学尝试运用课堂上学到的方法,自主研究函数y=![]() 的图象与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
的图象与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
(1)函数y=![]() 自变量的取值范围是 ;
自变量的取值范围是 ;
(2)下表列出了y与x的几组对应值:
x | … | ﹣2 | ﹣ | m | ﹣ | ﹣ |
|
| 1 |
| 2 | … |
y | … |
|
| 1 |
| 4 | 4 |
| 1 |
|
| … |
表中m的值是 ;
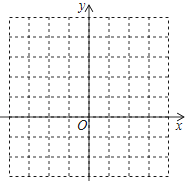
(3)如图,在平面直角坐标系xOy中,描出以表中各组对应值为坐标的点,试由描出的点画出该函数的图象;
(4)结合函数y=![]() 的图象,写出这个函数的性质: .(只需写一个)
的图象,写出这个函数的性质: .(只需写一个)
【题目】近几年,国内快递业务快速发展,由于其便捷、高效,人们越来越多地通过快递公司代办点来代寄包裹.某快递公司某地区一代办点对60天中每天代寄的包裹数与天数的数据(每天代寄包裹数、天数均为整数)统计如下:
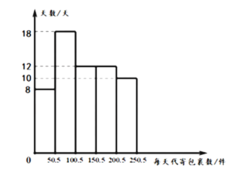
(1)求该数据中每天代寄包裹数在![]() 范围内的天数;
范围内的天数;
(2)若该代办点对顾客代寄包裹的收费标准为:重量小于或等于1千克的包裹收费8元;重量超1千克的包裹,在收费8元的基础上,每超过1千克(不足1千克的按1千克计算)需再收取2元.
①某顾客到该代办点寄重量为1.6千克的包裹,求该顾客应付多少元费用?
②这60天中,该代办点为顾客代寄的包表中有一部分重量超过2千克,且不超过5千克.现从中随机抽取40件包裹的重量数据作为样本,统计如下:
重量G(单位:千克) |
|
|
|
件数(单位:件) | 15 | 10 | 15 |
求这40件包裹收取费用的平均数.