题目内容
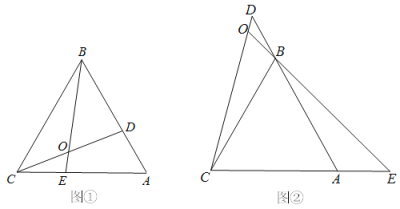
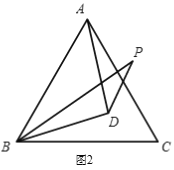
【题目】在利用构造全等三角形来解决的问题中,有一种典型的利用倍延中线的方法,例如:在△ABC中,AB=8,AC=6,点D是BC边上的中点,怎样求AD的取值范围呢?我们可以延长AD到点E,使AD=DE,然后连接BE(如图①),这样,在△ADC和△EDB中,由于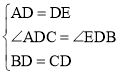 ,∴△ADC≌△EDB,∴AC=EB,接下来,在△ABE中通过AE的长可求出AD的取值范围.
,∴△ADC≌△EDB,∴AC=EB,接下来,在△ABE中通过AE的长可求出AD的取值范围.
请你回答:
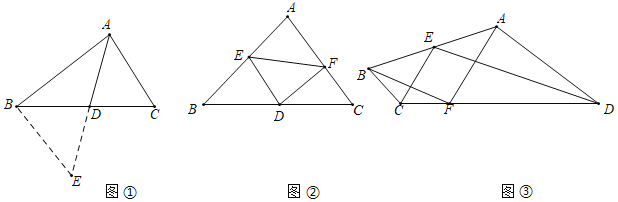
(1)在图①中,中线AD的取值范围是 .
(2)应用上述方法,解决下面问题
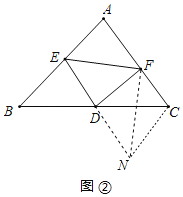
①如图②,在△ABC中,点D是BC边上的中点,点E是AB边上的一点,作DF⊥DE交AC边于点F,连接EF,若BE=4,CF=2,请直接写出EF的取值范围.
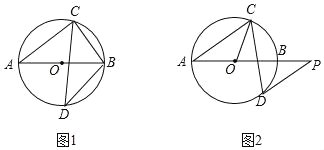
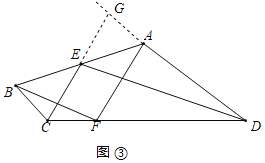
②如图③,在四边形ABCD中,∠BCD=150°,∠ADC=30°,点E是AB中点,点F在DC上,且满足BC=CF,DF=AD,连接CE、ED,请判断CE与ED的位置关系,并证明你的结论.
【答案】(1)1<AD<7;(2)①2<EF<6;②CE⊥ED,理由见解析
【解析】
(1)在△ABE中,根据三角形的三边关系定理即可得出结果;
(2)①延长ED到点N,使![]() ,连接CN、FN,由SAS证得
,连接CN、FN,由SAS证得![]() ,得出
,得出![]() ,由等腰三角形的性质得出
,由等腰三角形的性质得出![]() ,在△CFN中,根据三角形的三边关系定理即可得出结果;
,在△CFN中,根据三角形的三边关系定理即可得出结果;
②延长CE与DA的延长线交于点G,易证DG∥BC,得出![]() ,由ASA证得
,由ASA证得![]() ,得出
,得出![]() ,即可证得
,即可证得![]() ,由
,由![]() ,根据等腰三角形的性质可得出
,根据等腰三角形的性质可得出![]() .
.
(1)在△ABE中,由三角形的三边关系定理得:![]()
![]() ,即
,即![]()
![]() ,即
,即![]()
故答案为:![]() ;
;
(2)①如图②,延长ED到点N,使![]() ,连接CN、FN
,连接CN、FN
∵点D是BC边上的中点
![]()
在△NDC和△EDB中,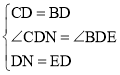
![]()
![]()
![]()
![]() 是等腰三角形,
是等腰三角形,![]()
在△CFN中,由三角形的三边关系定理得:![]()
![]() ,即
,即![]()
![]() ;
;
②![]() ;理由如下:
;理由如下:
如图③,延长CE与DA的延长线交于点G
∵点E是AB中点
![]()
![]()
![]()
![]()
在△GAE和△CBE中,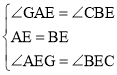
![]()
![]()
![]()
![]() ,即
,即![]()
![]()
![]() .(等腰三角形的三线合一)
.(等腰三角形的三线合一)

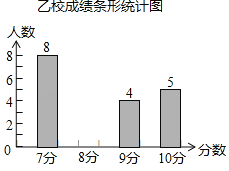
【题目】甲、乙两校参加学生英语口语比赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分),乙校平均分是8.3分,乙校的中位数是8分.依据统计数据绘制了如下尚不完整的甲校成绩统计表和乙校成绩统计图;
甲校成绩统计表
分数 | 7分 | 8分 | 9分 | 10分 |
人数 | 11 | 0 | ■ | 8 |
(1)请你将乙校成绩统计图直接补充完整;
(2)请直接写出甲校的平均分是 ,甲校的中位数是 ,甲校的众数是 ,从平均分和中位数的角度分析 校成绩较好(填“甲”或“乙”).