题目内容
【题目】在平行四边形ABCD中,连接BD,过点B作BE⊥BD于点B交DA的延长线于点E,过点B作BG⊥CD于点G.
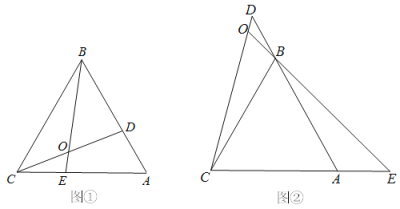
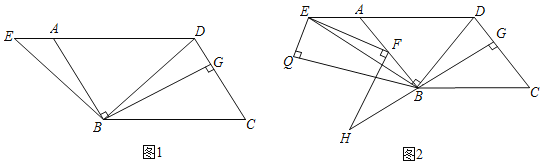
(1)如图1,若∠C=60°,∠BDC=75°,BD=6![]() ,求AE的长度;
,求AE的长度;
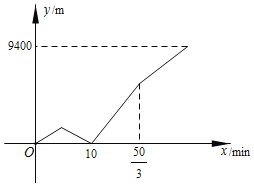
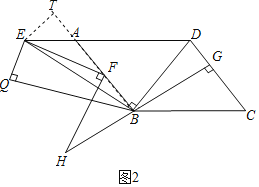
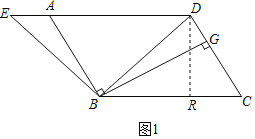
(2)如图2,点F为AB边上一点,连接EF,过点F作FH⊥FE于点F交GB的延长线于点H,在△ABE的异侧,以BE为斜边作Rt△BEQ,其中∠Q=90°,若∠QEB=∠BDC,EF=FH,求证:BF+BH=BQ.
【答案】(1)6﹣2![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)根据平行四边形性质可证:△BDE是等腰直角三角形,运用勾股定理可求DE和AD,AE即可求得;
(2)过点E作ET⊥AB交BA的延长线于T,构造直角三角形,由平行四边形性质及直角三角形性质可证:△BEQ≌△BET(AAS),△BFH≌△TEF(AAS),进而可证得结论.
解:(1)如图1,过点D作DR⊥BC于R,
∵ABCD是平行四边形
∴AB∥CD,AD∥BC,AD=BC
∵∠C=60°,∠BDC=75°,
∴∠CBD=180°﹣(∠C+∠BDC)=45°
∴∠ADB=∠CBD=45°
∵BE⊥BD
∴∠DBE=90°
∴∠E=∠BDE=45°
∴DE=![]() BD=12
BD=12
∵DR⊥BC
∴∠BRD=∠CRD=90°
∴∠BDR=∠CBD=45°,
∴DR=BR
由勾股定理可得![]() 即
即![]()
∴DR=BR=6
∵∠C=60°
∴∠CDR=90°﹣60°=30°
∴CR=2![]() ,CD=4
,CD=4![]()
∴AD=BC=DR+CR=6+2![]() ,
,
∴AE=DE﹣AD=12﹣(6+2![]() )=6﹣2
)=6﹣2![]() ;
;
(2)如图2,过点E作ET⊥AB交BA的延长线于T,则∠T=90°
∵ABCD是平行四边形
∴AB∥CD,
∴∠ABD=∠BDC
∵∠QEB=∠BDC
∴∠QEB=∠ABD
∵BG⊥CD,BE⊥BD,FH⊥FE
∴∠BGC=∠ABG=∠DBE=∠EFH=∠Q=90°
∴∠EBT+∠BET=∠EBT+∠ABD=∠EFT+∠BFH=∠EFT+∠FET=90°,
∴∠BET=∠ABD=∠QEB,∠BFH=∠FET
∵BE=BE,EF=FH
∴△BEQ≌△BET(AAS),△BFH≌△TEF(AAS)
∴BQ=BT,BH=FT
∵BF+FT=BT
∴BF+BH=BQ.

【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.