题目内容
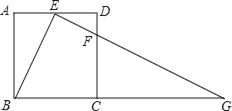
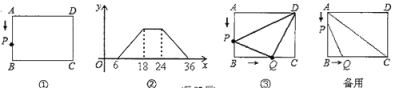
【题目】如图①,在矩形![]() 中,动点
中,动点![]() 从
从![]() 出发,以相同的速度,沿
出发,以相同的速度,沿![]() 方向运动到点
方向运动到点![]() 处停止.设点
处停止.设点![]() 运动的路程为
运动的路程为![]() ,
, ![]() 面积为
面积为![]() ,
,![]() 与
与![]() 的函数图象如图②所示.
的函数图象如图②所示.
(1)矩形![]() 的面积为 ;
的面积为 ;
(2)如图③,若点![]() 沿
沿![]() 边向点
边向点![]() 以每秒1个单位的速度移动,同时,点
以每秒1个单位的速度移动,同时,点![]() 从点
从点![]() 出发沿
出发沿![]() 边向点
边向点![]() 以每秒2个单位的速度移动.如果
以每秒2个单位的速度移动.如果![]() 、
、![]() 两点在分别到达
两点在分别到达![]() 、
、![]() 两点后就停止移动,回答下列问题:
两点后就停止移动,回答下列问题:
①当运动开始![]() 秒时,试判断
秒时,试判断![]() 的形状;
的形状;
②在运动过程中,是否存在这样的时刻,使以![]() 为圆心,
为圆心,![]() 的长为半径的圆与矩形
的长为半径的圆与矩形![]() 的对角线
的对角线![]() 相切,若存在,求出运动时间;若不存在,请说明理由.
相切,若存在,求出运动时间;若不存在,请说明理由.
【答案】(1)72;(2)①![]() 为直角三角形;②不存在
为直角三角形;②不存在
【解析】
(1)通过图形可以求出矩形的长和宽,然后计算矩形的面积;
(2)①通过速度,可计算出PD、PQ、DQ的长,然后建立勾股定理,可得△PDQ为直角三角形;
②过Q作QM⊥AC,通过计算QM和PQ的长,利用两条线段长度相等,可列出方程,计算方程的解就是运动时间;若方程无解,则情况不成立.
解:(1)由图象②可得长方形的长和宽为12和6,则面积为:12×6=72;
(2)①由题意可知:AP=![]() ,BP=
,BP=![]() ,BQ=3,CQ=9
,BQ=3,CQ=9
∴在Rt△APD中:![]()
在Rt△BPQ中:![]()
在Rt△CDQ中:![]()
∵![]() 即:
即:![]()
∴△DPQ为直角三角形
②不存在.理由:假设存在,连接AC,过点Q作QM垂直于AC垂足为点M.
则QM=PQ,即得:![]()
即![]()
化简得:![]()
∵△<0
∴此方程无解,即不存在

练习册系列答案
相关题目