题目内容
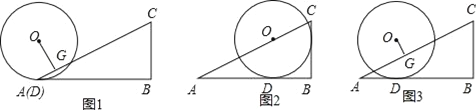
【题目】如图,△ABC中,∠B=90°,tan∠BAC=![]() ,半径为2的⊙O从点A开始(图1),沿AB向右滚动,滚动时始终与AB相切(切点为D);当圆心O落在AC上时滚动停止,此时⊙O与BC相切于点E(图2).作OG⊥AC于点G.
,半径为2的⊙O从点A开始(图1),沿AB向右滚动,滚动时始终与AB相切(切点为D);当圆心O落在AC上时滚动停止,此时⊙O与BC相切于点E(图2).作OG⊥AC于点G.
(1)利用图2,求cos∠BAC的值;
(2)当点D与点A重合时(如图1),求OG;
(3)如图3,在⊙O滚动过程中,设AD=x,请用含x的代数式表示OG,并写出x的取值范围.
【答案】(1)cos∠BAC=![]() ;(2)OG=
;(2)OG=![]() ;(3)OG=﹣
;(3)OG=﹣![]() x+
x+![]() ,x的取值范围是:0≤x≤4.
,x的取值范围是:0≤x≤4.
【解析】整体分析:
(1)连接OD,Rt△AOD中用勾股定理求OA,用余弦的定义求解;(2)连接OA,则∠AOG=∠BAC,在Rt△OAG中,用∠AOG的余弦求解;(3)连接OD交AC于点F,用x表示出OF,由∠FOG=∠BAC,利用∠FOG的余弦求解.
解:(1)如图2,连接OD,
∵⊙O与AB相切,∴OD⊥AB,
∵tan∠BAC=![]() ,OD=2,∴AD=4,OA=
,OD=2,∴AD=4,OA=![]() ,
,
∴cos∠BAC=![]() =
=![]() ;
;
(2)如图1,连接OA,
∵⊙O与AB相切,∴OA⊥AB,
又∵OG⊥AC,∴∠AOG=90°﹣∠OAG=∠BAC,
∴cos∠AOG=cos∠BAC=![]() .
.
∵cos∠AOG=![]() ,
,
∴OG=OAcos∠AOG=2×![]() =
=![]() ;
;
(3)如图3,连接OD交AC于点F,
∵⊙O与AB相切,∴OD⊥AB,∴∠FOG=90°﹣∠OFG,
又∵OG⊥AC,∴∠BAC=90°﹣∠AFD,
又∵∠OFG=∠AFD,∴∠FOG=∠BAC,
∵tan∠BAC=![]() ,
,
∴FD=ADtan∠BAC=![]() x,
x,
∴OF=2﹣![]() x,∵cos∠BAC=cos∠FOG=
x,∵cos∠BAC=cos∠FOG=![]() ,
,
∴OG=OFcos∠FOG=![]() (2﹣
(2﹣![]() x)=﹣
x)=﹣![]() x+
x+![]() ,x的取值范围是:0≤x≤4.
,x的取值范围是:0≤x≤4.

 口算能手系列答案
口算能手系列答案【题目】“十年树木,百年树人”,教师的素养关系到国家的未来.我市某区招聘音乐教师采用笔试、专业技能测试、说课三种形式进行选拔,这三项的成绩满分均为100分,并按2∶3∶5的比例纳入总分.最后,按照成绩的排序从高到低依次录取.该区要招聘2名音乐教师,通过笔试、专业技能测试筛选出前6名选手进入说课环节,这6名选手的各项成绩见下表:
序号 | 1 | 2 | 3 | 4 | 5 | 6 |
笔试成绩/分 | 66 | 90 | 86 | 64 | 65 | 84 |
专业技能测试成绩/分 | 95 | 92 | 93 | 80 | 88 | 92 |
说课成绩/分 | 85 | 78 | 86 | 88 | 94 | 85 |
(1)写出说课成绩的中位数、众数;
(2)已知序号为1,2,3,4号选手的成绩分别为84.2分,84.6分,88.1分,80.8分,请你判断这6名选手中序号是多少的选手将被录用?为什么?