Question

【题目】某校八年级数学小组在课外活动中，研究了同一坐标系中两个反比例函数与（）在第一象限图像的性质，经历了如下探究过程：

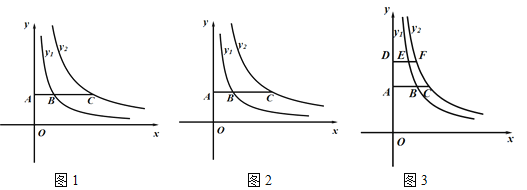
操作猜想：（1）如图1，当，时，在y轴的正半轴上取一点A作x轴的平行线交于点B，交于点C．当OA＝1时，＝ ；当OA＝3时，＝ ；当OA＝a时，猜想＝ ．

数学思考：（2）在y轴的正半轴上任意取点A作x轴的平行线，交于点B、交于点C，请用含、的式子表示的值，并利用图2加以证明．

推广应用：（3）如图3，若，，在y轴的正半轴上分别取点A、D（OD＞OA）作x轴的平行线，交于点B、E，交于点C、F，是否存在四边形ADFB是正方形？如果存在，求OA的长和点B的坐标；如果不存在，请说明理由．

Answer 1

【答案】（1）2；2；2；（2），证明见解析；（3）OA=4，点B的坐标为（2，4）．

【解析】

（1）只需根据ABOA=2及ACOA=6就可解决问题；

（2）由ABOA=k1及ACOA=k2可得BCOA=k2-k1，就可得到；

（3）设点B的坐标为（a，b）（a＞0，b＞0），则有DF=DA=AB=a，OA=b，从而可得到点F的坐标为（a，a+b）．由k2=12及可求得k1=8．然后根据点B在y=图象上，点F在y=图象上，可得到ab=8，a（a+b）=12，从而求出a、b的值，就可解决问题．

（1）当OA=1时，由ABOA=2得AB=2，由ACOA=6得AC=6，则有BC=AC-AB=4，所以；

当OA=3时，由ABOA=2得AB=，由ACOA=6得AC=2，则有BC=AC-AB=，所以；

当OA=a时，猜想：．

（2）．

证明：∵ABOA=k1，ACOA=k2，

∴ACOA-ABOA=BCOA=k2-k1，

∴．

（3）若四边形ADFB是正方形，

设点B的坐标为（a，b）（a＞0，b＞0），

则有DF=DA=AB=a，OA=b，OD=a+b，

∴点F的坐标为（a，a+b）．

∵k2=12，，

∴，

解得：k1=8．

∵点B在y=图象上，点F在y=图象上，

∴ab=8，a（a+b）=12，

∴a2=12-8=4/span>，

∴a=2，

∴b=4，

∴OA=4，点B的坐标为（2，4）．