题目内容
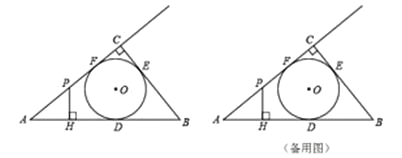
【题目】如图,![]() 的内切圆
的内切圆![]() 与
与![]() ,
,![]() ,
,![]() 分别相切于点
分别相切于点![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,点
,点![]() 在射线
在射线![]() 上运动,过点
上运动,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
(1)直接写出线段![]() ,
,![]() 及
及![]() 半径的长:
半径的长:
(2)设![]() ,
,![]() . 求
. 求![]() 关于
关于![]() 的函数关系式:
的函数关系式:
(3)当![]() 与
与![]() 相切时,求相应的
相切时,求相应的![]() 值.
值.
【答案】(1)![]() ,
,![]() ,
,![]() 的半径长为1;(2)
的半径长为1;(2)![]() (
(![]() ),
),![]() (
(![]() );(3)
);(3)![]() 的值为
的值为![]() 或1.
或1.
【解析】
(1)由勾股定理求AC的长度;设⊙O的半径为r,则r=![]() (AC+BC-AB);根据圆的切线定理、正方形的判定定理知四边形CEOF是正方形;然后由正方形的性质证得CF=OF=1,则由图中线段间的和差关系即可求得AD的长度;
(AC+BC-AB);根据圆的切线定理、正方形的判定定理知四边形CEOF是正方形;然后由正方形的性质证得CF=OF=1,则由图中线段间的和差关系即可求得AD的长度;
(2)分类讨论:①当点P在线段AC上时,通过相似三角形△AHP∽△ACB的对应边成比例知,![]() ,将“PH=x,PC=y”代入求出即可求得y关于x的函数关系式;②当点P在线段AC的延长线上时,同理,利用相似三角形的性质求得y关于x的函数关系式;
,将“PH=x,PC=y”代入求出即可求得y关于x的函数关系式;②当点P在线段AC的延长线上时,同理,利用相似三角形的性质求得y关于x的函数关系式;
(3)根据题意,可分成两种情况进行①当点![]() 在线段
在线段![]() 上时,
上时,![]() 与
与![]() 相切;②当点
相切;②当点![]() 在
在![]() 的延长线上时,
的延长线上时,![]() 与
与![]() 相切;结合图形和所学的性质,即可求得y值.
相切;结合图形和所学的性质,即可求得y值.
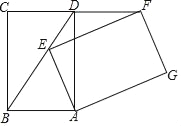
解:(1)如图1,连接AO、DO.设⊙O的半径为r.
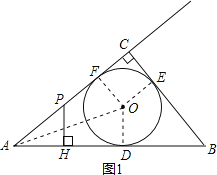
在Rt△ABC中,由勾股定理得AC=![]() ,
,
则⊙O的半径r=![]() (AC+BC-AB)=
(AC+BC-AB)=![]() ×(4+3-5)=1;
×(4+3-5)=1;
∵CE、CF是⊙O的切线,∠ACB=90°,
∴∠CFO=∠FCE=∠CEO=90°,OF=OE,
∴四边形CEOF是正方形,
∴CF=OF=1;
又∵AD、AF是⊙O的切线,
∴AF=AD;
∴AF=AC-CF=AC-OF=4-1=3,
即AD=3;
∴![]() ,
,![]() ,
,![]() 的半径长为1.
的半径长为1.
(2)①如图,若点![]() 在线段
在线段![]() 上时,
上时,
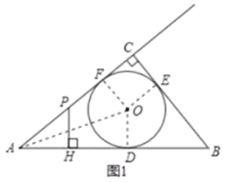
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]()
∴![]() ,
,
∴![]() 与
与![]() 的函数关系式是:
的函数关系式是:![]() (
(![]() );
);
②同理,当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,
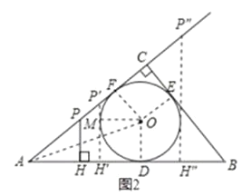
![]() ,此时
,此时![]()
则![]() ,有
,有![]()
∴![]() ,即
,即![]() 与
与![]() 的函数关系式是:
的函数关系式是:![]() (
(![]() );
);
(3)①当点![]() 在线段
在线段![]() 上时,如图2,
上时,如图2,![]() 与
与![]() 相切.
相切.

∵![]() ,
,![]() ,
,
∴四边形![]() 是正方形,
是正方形,
∴![]() ;
;
由(1)知,四边形![]() 是正方形,
是正方形,
![]() ,
,
∴![]() ,即
,即![]() ;
;
即![]() ,解得
,解得![]() ;
;
②当点![]() 在
在![]() 的延长线上时,如图,
的延长线上时,如图,

∴![]() 与
与![]() 相切,此时
相切,此时![]() .
.
综上所示,当![]() 与
与![]() 相切时,
相切时,![]() 的值为
的值为![]() 或1.
或1.