题目内容
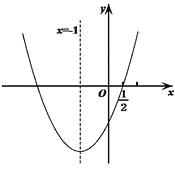
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列5个结论:①
,下列5个结论:①![]() ; ②
; ②![]() ; ③
; ③![]() ;④
;④![]() ; ⑤
; ⑤![]() ,其中正确的结论为________________.(注:只填写正确结论的序号)
,其中正确的结论为________________.(注:只填写正确结论的序号)
【答案】②④.
【解析】
根据抛物线开口方向得到a>0,根据抛物线对称轴为直线x=-![]() =-1得到b=2a,则b>0,根据抛物线与y轴的交点在x轴下方得到c<0,所以abc<0;由x=
=-1得到b=2a,则b>0,根据抛物线与y轴的交点在x轴下方得到c<0,所以abc<0;由x=![]() ,y=0,得到
,y=0,得到![]() a+
a+![]() b+c=0,即a+2b+4c=0;由a=
b+c=0,即a+2b+4c=0;由a=![]() b,a+b+c>0,得到
b,a+b+c>0,得到![]() b+2b+c>0,即3b+2c>0;由x=-1时,函数最大小,则a-b+c<m2a-mb+c(m≠1),即a-b≤m(am-b).
b+2b+c>0,即3b+2c>0;由x=-1时,函数最大小,则a-b+c<m2a-mb+c(m≠1),即a-b≤m(am-b).
解:∵抛物线开口向上,
∴a>0,
∵抛物线对称轴为直线x=-![]() =-1,
=-1,
∴b=2a,则2a-b=0,所以③错误;
∴b>0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc<0,所以①错误;
∵x=![]() 时,y=0,
时,y=0,
∴![]() a+
a+![]() b+c=0,即a+2b+4c=0,所以②正确;
b+c=0,即a+2b+4c=0,所以②正确;
∵a=![]() b,a+b+c>0,
b,a+b+c>0,
∴![]() b+2b+c>0,即3b+2c>0,所以④正确;
b+2b+c>0,即3b+2c>0,所以④正确;
∵x=-1时,函数最大小,
∴a-b+c<m2a-mb+c(m≠1),
∴a-b≤m(am-b),所以⑤错误.
故答案为②④.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目