题目内容
【题目】将矩形ABCD绕点A顺时针旋转得到矩形AEFG,点E在BD上;
(1)求证:FD=AB;(2)连接AF,求证:∠DAF=∠EFA.
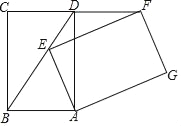
【答案】(1)见解析;(2)见解析.
【解析】
(1)先运用SAS判定△AED≌△FDE,可得DF=AE,再根据AE=AB=CD,即可得出AB=DF;
(2)设EF与AD交点为点H,由△AED≌△FDE,可得∠EDA=∠DEF,EF=AD,可证HF=HA,即可得∠DAF=∠EFA.
解:(1)由旋转可得,AE=AB,∠AEF=∠ABC=∠DAB=90°,EF=BC=AD,
∴∠AEB=∠ABE,
又∵∠ABE+∠EDA=90°=∠AEB+∠DEF,
∴∠EDA=∠DEF,
又∵DE=ED,
∴△AED≌△FDE(SAS),
∴DF=AE,
又∵AE=AB=CD,
∴AB=DF;
(2)如图:设EF与AD交点为点H
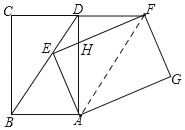
∵△AED≌△FDE
∴∠EDA=∠DEF,EF=AD
∴HE=HD
又∵EF=AD
∴EF﹣HE=AD﹣HD
即HF=HA
∴∠DAF=∠EFA

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在 点
在 点![]() 左侧),对称轴为直线
左侧),对称轴为直线![]() .
.
(1)![]() 的值为 ,在坐标系中利用描点法画出此抛物线;
的值为 ,在坐标系中利用描点法画出此抛物线;
| ··· | ··· | |||||
| ··· | ··· |
(2)若直线![]() 过点
过点![]() 且与抛物线交于点
且与抛物线交于点![]() ,请根据图象写出:当
,请根据图象写出:当![]() 时,
时,![]() 的取值范围是 .
的取值范围是 .