题目内容
【题目】如图,在平面直角坐标系中点A的坐标为(3,6),点B(6,0),C是线段OB上一动点(不与O,B重合),过C,O两点的二次函数y1和过C,B两点的二次函数y2的图像开口均向下,它们的顶点分别为OA,AB边上的E,F两点,点C从点O到点B运动过程中,阴影部分的面积大小变化情况是( )
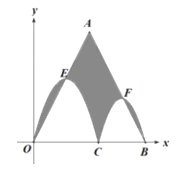
A.不变B.先增大再减小C.先减小再增大D.无法确定
【答案】B
【解析】
根据抛物线的对称性,阴影部分的面积就是平行四边形AECF的面积,设平行四边形AECF的面积为y,OC的长为![]() ,根据相似三角形对应高的比等于相似比,求得y关于
,根据相似三角形对应高的比等于相似比,求得y关于![]() 的函数关系式即可求解.
的函数关系式即可求解.
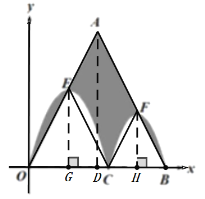
连接EC、FC,
∵抛物线的顶点E,F分别在OA,AB边上,
根据抛物线的对称性,知:EO=EC,FC=FB,
∴![]() 和
和![]() 都是等腰三角形,
都是等腰三角形,
利用割补法得:阴影部分的面积就是平行四边形AECF的面积,
设平行四边形AECF的面积为y,OC的长为![]() ,
,
分别过点E、F、A作OB的垂线,垂足分别为G、H、D,
∵点A的坐标为(3,6),点B(6,0),
∴OD=3,OB=6,
∵OD=DB=![]() OB=3,且AD⊥OB,
OB=3,且AD⊥OB,
∴![]() 是等腰三角形,
是等腰三角形,
∴![]() 和
和![]() 、
、![]() 都是底角相等的等腰三角形,
都是底角相等的等腰三角形,
∴![]() ,
,
根据相似三角形对应高的比等于相似比,得:
![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
化简得:![]() (
(![]() )
)
∵![]() ,对称轴为
,对称轴为![]() ,
,
∴![]() 的值先增大后减小,
的值先增大后减小,
故选:B.

 名校课堂系列答案
名校课堂系列答案【题目】七(2)班共有50名学生,老师安排每人制作一件![]() 型或
型或![]() 型的陶艺品,学校现有甲种制作材料36
型的陶艺品,学校现有甲种制作材料36![]() ,乙种制作材料29
,乙种制作材料29![]() ,制作
,制作![]() 、
、![]() 两种型号的陶艺品用料情况如下表:
两种型号的陶艺品用料情况如下表:
需甲种材料 | 需乙种材料 | |
1件 | 0.9 | 0.3 |
1件 | 0.4 | 1 |
(1)设制作![]() 型陶艺品
型陶艺品![]() 件,求
件,求![]() 的取值范围;
的取值范围;
(2)请你根据学校现有材料,分别写出七(2)班制作![]() 型和
型和![]() 型陶艺品的件数.
型陶艺品的件数.
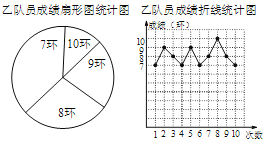
【题目】某射击队准备从甲、乙两名队员中选取一名队员代表该队参加比赛,特为甲、乙两名队员举行了一次选拔赛,要求这两名队员各射击10次.比赛结束后,根据比赛成绩情况,将甲、乙两名队员的比赛成绩制成了如下的统计图(表):
甲队员的成绩统计表
成绩(单位:环) | 7 | 8 | 9 | 10 |
次数(单位:次) | 5 | 1 | 2 | 2 |
(1)在图1中,求“8环”所在扇形的圆心角的度数;
(2)经过整理,得到的分析数据如表,求表中的a、b、c的值.
队员 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 8 | 7.5 | 7 | c |
乙 | a | b | 7 | 1 |
(3)根据甲、乙两名队员的成绩情况,该射击队准备选派乙参加比赛,请你写出一条射击队选派乙的理由.