Question

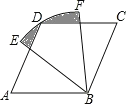
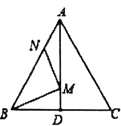
【题目】如图，在等边中，已知，为上一点，且，的平分线交于点，是AD上的动点，连结，，则的最小值是( )

A. 8B. 10C. D.

Answer 1

【答案】D

【解析】

连接CN，与AD交于点M，取BN中点E，连接DE，由等边三角形的性质可得AD为BC的垂直平分线，可知BM=CM，则CN就是BM+MN的最小值．根据三角形中位线的性质可得DM=AD，CM=CN，利用勾股定理可求出CM的长，进而可得CN的长，即可得答案.

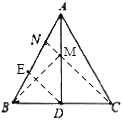
连接CN，与AD交于点M，取BN中点E，连接DE．

∵AB=AC，AD是∠BAC的角平分线，

∴AD是BC的垂直平分线，

∴BM=CM，

∴CN就是BM+MN的最小值．

∵等边△ABC的边长为6，AN=2，

∴BN=AC-AN=6-2=4，

∴BE=EN=AN=2，

又∵AD是BC边上的中线，

∴DE是△BCN的中位线，

∴CN=2DE，CN∥DE，

又∵N为AE的中点，

∴M为AD的中点，

∴MN是△ADE的中位线，

∴DE=2MN，

∴CN=2DE=4MN，

∴CM=CN．

在直角△CDM中，CD=BC=3，DM=AD=，

∴CM==

∴CN=CM=，

∵BM+MN=CN，

∴BM+MN的最小值为.

故选D.