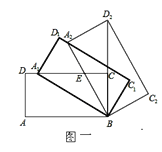
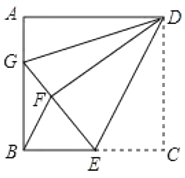
题目内容
【题目】如图![]() 中,
中,![]() ,P是斜边AC上一个动点,以即为直径作
,P是斜边AC上一个动点,以即为直径作![]() 交BC于点D,与AC的另一个交点E,连接DE.
交BC于点D,与AC的另一个交点E,连接DE.
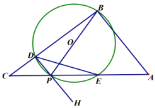
(1)当![]() 时,
时,
①若![]() ,求
,求![]() 的度数;
的度数;
②求证![]() ;
;
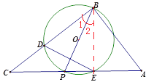
(2)当![]() ,
,![]() 时,
时,
①是含存在点P,使得![]() 是等腰三角形,若存在求出所有符合条件的CP的长;
是等腰三角形,若存在求出所有符合条件的CP的长;
②以D为端点过P作射线DH,作点O关于DE的对称点Q恰好落在![]() 内,则CP的取值范围为________.(直接写出结果)
内,则CP的取值范围为________.(直接写出结果)
【答案】(1)①40°;②详见解析;(2)①7,10,12.5;②![]()
【解析】
(1)①由BP是直径可得![]() ,根据
,根据![]() 得
得 ![]() 并可得
并可得![]() ,
, ![]() ,
,![]() ,根据三角形的内角和定理得
,根据三角形的内角和定理得![]() ;②由
;②由![]() ,得到
,得到![]() ,根据
,根据![]() ,
,![]() ,
,![]() ,得到,
,得到,![]() 由等角对等边得
由等角对等边得![]() ;
;
(2)①分三种情况:(一)当![]() 时,(二)当
时,(二)当![]() 时,(三)当
时,(三)当![]() 时,分别进行讨论求解即可;
时,分别进行讨论求解即可;
②分三种情况讨论:(一)当Q点在P点上时;(二)当Q点在PC上时(三)当Q点在PH上时,分别讨论,求出CP的值即可.
24.解(1)①连结BE,∵BP是直径∴![]()
∵![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() ∴
∴![]()
∴![]()
②∵![]() ,∴
,∴![]()
![]() ,
,![]()
又∵![]()
∴![]()
∴![]()
(2)①由![]() ,
,![]() ,可以求得
,可以求得![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]()
∴![]()
当![]() 是等腰三角形时,有三种情况:(一)
是等腰三角形时,有三种情况:(一)![]() ,(二)
,(二)![]() ,(三)
,(三)![]()
(一)当![]() 时,
时,![]()
∴![]() ,
,
∴![]()
∴![]()
(二)当![]() 时,可知点D是
时,可知点D是![]() 斜边的中线,
斜边的中线,
∴![]() ,
,
∴![]()
∴![]()
(三)当![]() 时,
时,
作![]() ,则H是BD中点,
,则H是BD中点,
可以求得![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]()
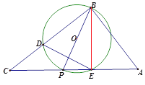
②(一)当O点的对称点Q在P点上时,B,O,Q三点共线,
如图示
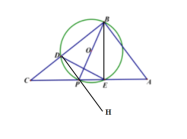
∴![]() ,且BP平分DE,由等腰三角形的性质可知
,且BP平分DE,由等腰三角形的性质可知
∴![]()
由(1)可知CP=7;
(二)当O点的对称点Q不在P点上,而在PC上时,此情况Q点并不在![]() 上
上
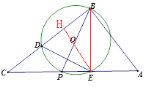
(三)当O点的对称点Q不在P点上,而在PH上时,B,O,Q三点不共线,
如图示
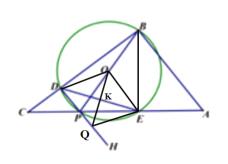
∵![]() ,
,![]() ,且
,且![]()
∴四边形DOEQ是菱形,
∴![]()
∵![]()
∴![]()
又∵OE,OD,OB均为外接圆的半径,
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴由(1)可知,![]()
∴![]()

【题目】某校为了解中学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了![]() 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
节目 | 人数(名) | 百分比 |
最强大脑 |
|
|
朗读者 |
|
|
中国诗词大会 |
|
|
出彩中国人 |
|
|
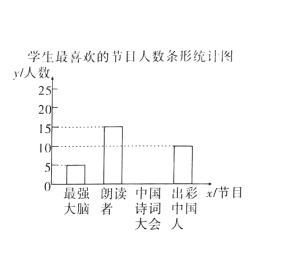
根据以上提供的信息.解答下列问题:
![]() ,
,![]() ,
,![]() ;
;
![]() 补全上面的条形统计图;
补全上面的条形统计图;
![]() 名女同学.其余为男同学,现要从中随机抽取
名女同学.其余为男同学,现要从中随机抽取![]() 名同学代表学校参加市里组织的竞赛活动,请求出所抽取的
名同学代表学校参加市里组织的竞赛活动,请求出所抽取的![]() 名同学恰好是
名同学恰好是![]() 名男同学和
名男同学和![]() 名女同学的概率.
名女同学的概率.