Question

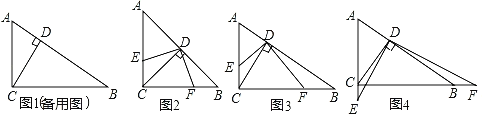
【题目】已知，如图一张三角形纸片ABC，边AB长为10cm，AB边上的高为15cm，在三角形内从左到右叠放边长为2的正方形小纸片，第一次小纸片的一条边都在AB上，依次这样往上叠放上去，则最多能叠放的正方形的个数是( ).

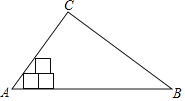
A. 12B. 13C. 14D. 15

Answer 1

【答案】C

【解析】

根据相似的判定与性质每一层的靠上的边的长度，从而判定可放置的正方形的个数及层数．

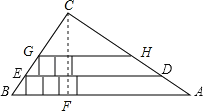
解：作CF⊥AB于点F，

设最下边的一排小正方形的上边的边所在的直线与△ABC的边交于D、E，

∵DE∥AB，

∴，即，

解得：DE＝，而整数部分是4，

∴最下边一排是4个正方形．

第二排正方形的上边的边所在的直线与△ABC的边交于G、H．

则，解得GH＝，而整数部分是3，

∴第二排是3个正方形；

同理：第三排是：3个；

第四排是2个，

第五排是1个，

第六排是1个，则正方形的个数是：4+3+3+2+1+1＝14．

故选：C．