题目内容
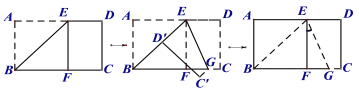
【题目】已知线段AB⊥直线l于点B,点M在直线l上,分别以AB、AM为边作等边△ABC和等边△AMN,直线CN交直线l于点D.
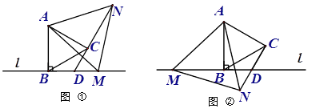
(1)当点M在AB右侧时,如图①,试探索线段CN、CD、DM的数量关系,并说明理由;
(2)当点M在AB左侧时,如图②,(1)中线段CN、CD、DM的数量关系仍然成立吗?若不成立,写出新的数量关系;
(3)若BM=2BD,DN=9,则CD= .
【答案】(1)MD=CN-CD;理由见解析;
(2)(1)中的数量关系不成立,MD=CN+CD;理由见解析;
(3)CD=3或9
【解析】
(1)如图①中,设AM交ND于O.首先证明△ABM≌△ACN(SAS),推出BM=NC,再证明BD=CD即可得到MD=CN-CD;
(2)如图②, 设AM交ND于O.类似(1)的证明方法,先证明△ABM≌△ACN(SAS),得到CN=BM,再证明CD=BD,可得到MD=CN+CD;
(3)分图①,图②两种情形,设BD=CD=x,则BM=2x,列出方程分别求解即可.
(1)MD=CN-CD;理由是:
如图①中,设AM交ND于O.
∵△ABC,△AMN都是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
∴△ABM≌△ACN(SAS),
∴CN=BM,
∴∠ANO=∠DMO,
∵∠AON=∠DOM,
∴∠ODM=∠OAN=60°,
∵AB⊥BC,
∴∠ABM=90°,
∵∠ABC=60°,
∴∠CBD=30°,
∵∠ODM=∠CBD+∠BCD,
∴∠DBC=∠DCB=30°,
∴CD=BD,
∴MD=CN-CD
(2)不成立,MD=CN+CD;
证明:如图②, 设AM交ND于O.

∵△ABC,△AMN都是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
∴△ABM≌△ACN(SAS),
∴CN=BM,
∴∠ANC=∠AMB,
∵∠AOM=∠DON,
∴∠ODN=∠OAM=60°,
∵AB⊥BD,
∴∠ABD=90°,
∵∠ABC=60°,
∴∠CBD=30°,
∵∠ODN=∠CBD+∠BCD,
∴∠DBC=∠DCB=30°,
∴CD=BD,
∴MD=MB+BD=CN+CD;
(3)分两种情况:
①如图①中,

∵BM=2BD,设BD=MD=CD=x,则BM=2x,
∵DN=9,BM=NC,
∴BM+CD=DN
∴2x+x=9,
∴x=3
∴CD=3.
②如图②中,设BD=CD=x,则BM=2x,

∵BM=NC,ND=9,
CD+DN= CN;
∴x+9=2x,
∴x=9,
∴CD=9,
综上所述,CD=3或9.
故答案为3或9.

【题目】如下表,方程1、方程2、方程3…是按照一定规律排列的一列方程。
(1)猜想方程1的解,并将它们的解填在表中的空白处。
序号 | 方程 | 方程的解( |
1 |
|
|
2 |
|
|
3 |
|
|
… | …… | …… |
(2)若方程![]()
![]() 的解是
的解是![]() ,猜想a,b的值。
,猜想a,b的值。
(3)请写出这列方程中的第n个方程和它的解。