题目内容
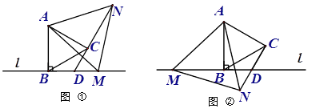
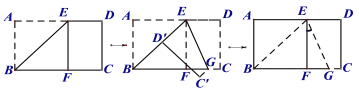
【题目】将长方形纸片ABCD沿过点B的直线折叠,使点A落在BC边上点F处,折痕为BE,再沿过点E的直线折叠,使点D落在BE边上点D’处,折痕为EG,展平纸片,则图中∠FEG= ______ °
【答案】22.5
【解析】
利用折叠的性质,可得∠AEB=45°,∠BEG=DEG,四边形ABFE是正方形,又由平角的定义即可求得∠DEG的度数,继而求得∠FEG的值.
解:根据题意得:
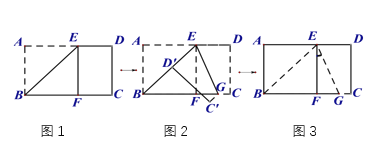
如图1:四边形ABFE是正方形,
∴∠AEB=∠FEB=45°,
如图3:∵EG是折痕,
∴∠BEG=DEG,
∵∠AEB=45°,∠AEB+∠BEG+∠DEG=180°,
∴∠DEG=67.5°,
∴∠FEG =90°-∠DEG=22.5°.
故答案为:22.5.

【题目】某公司生产A种产品,它的成本是6元/件,售价是8元/件,年销售量为5万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x万元,产品的年销售量将是原销售量的y倍,且y与x之间满足我们学过的二种函数(即一次函数和二次函数)关系中的一种,它们的关系如下表:
x(万元) | 0 | 0.5 | 1 | 1.5 | 2 | … |
y | 1 | 1.275 | 1.5 | 1.675 | 1.8 | … |
(1)求y与x的函数关系式(不要求写出自变量的取值范围)
(2)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润W(万元)与广告费用x(万元)的函数关系式,并计算每年投入的广告费是多少万元时所获得的利润最大?
(3)如果公司希望年利润W(万元)不低于14万元,请你帮公司确定广告费的范围.
【题目】2017年6月22日至7月2日,11天湖南地区持续降大到暴雨,总量达570亿立方米的雨水从天而降,倾泻到三湘大地,全省14个市州120个县(市、区)1621个多镇受灾,现有三批救灾物资从长沙岀发送往某受灾乡镇,前两批物资运货情况如图所示:
火车皮(单位:节) | 汽车(单位:辆) | 物质重量(单位:吨) | |
第一批 | 4 | 16 | 264 |
第二批 | 6 | 10 | 340 |
(1)每节火车皮和每辆汽车平均各能装多少吨物资?
(2)已知火车皮的装运费为30元吨,汽车的装运费为100元/吨.若第三批救灾物资需要5节火车皮和15辆汽车正好装完,共需要装运费多少元?