Question

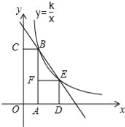
【题目】如图，在平面直角坐标系中，正方形中心在原点，且顶点的坐标为．动点分别从点同时出发，绕着正方形的边按顺时针方向运动，当点回到点时两点同时停止运动，运动时间为秒．连接，线段、与正方形的边围成的面积较小部分的图形记为．

（1）请写出点的坐标．

（2）若的速度均为1个单位长度秒，试判断在运动过程中，的面积是否发生变化，如果不变求出该值，如果变化说明理由．

（3）若点速度为2个单位长度秒，点为1个单位长度/秒，当的面积为时，求的值．

Answer 1

【答案】（1），，；（2）不变，理由详见解析；（3）或

【解析】

(1)利用正方形的性质，结合B、C、D的位置写出坐标即可；
(2)只要证明△OAP≌△OBQ，可得S△OAP=S△OBQ，推出SM=S△OAB= S正方形ABCD=1；
(3)分两种情形：①当点P在线段AB上，点Q在线段BC上时，②当点P、Q在CD上时，分别构建方程即可解决问题；

解：(1)由题意B(1,1)，C(1,1)，D(1,1)；
(2)M的面积不发生变化．
理由：如图，连接OA、OB．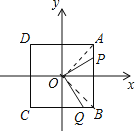

∵四边形ABCD是正方形，O是正方形的中心，
∴OA=OB，∠OAP=∠OBQ=45°，
∵AP=BQ，
∴△OAP≌△OBQ，
∴S△OAP=S△OBQ，
∴SM=S△OAB= S正方形ABCD=1，
∴M的面积S是定值，定值为1．
(3)①当点P在线段AB上，点Q在线段BC上时，连接OB，

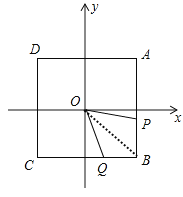
由题意得：SM=S△OBP+ S△OBQ=，即(22t)1+t1=，
解得t=；
②当点P、Q在CD上时，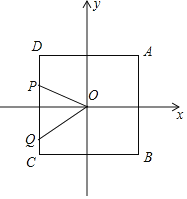

由题意得：SM=S△OPQ=，即(2tt1)·1=，
解得t=，
综上所述，t=或时，M的面积为．