题目内容
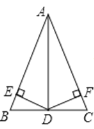
【题目】如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF.
求证:(1)△BDE≌△CDF;
(2)AD是△ABC的角平分线.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)求出BD=DC,∠DEB=∠DFC=90°,根据HL即可证Rt△BDE≌Rt△CDF;(2)由△BDE≌△CDF可得DE=DF,再根据角平分线的判定即可得AD是△ABC的角平分线.
(1)∵点D是BC的中点,
∴BD=DC,
∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°,
在Rt△BDE和Rt△CDF中
![]() ,
,
∴Rt△BDE≌Rt△CDF(HL);
(2)∵△BDE≌△CDF,
∴DE=DF,
又∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC,
即AD是△ABC的角平分线.

练习册系列答案
相关题目
【题目】2017年6月22日至7月2日,11天湖南地区持续降大到暴雨,总量达570亿立方米的雨水从天而降,倾泻到三湘大地,全省14个市州120个县(市、区)1621个多镇受灾,现有三批救灾物资从长沙岀发送往某受灾乡镇,前两批物资运货情况如图所示:
火车皮(单位:节) | 汽车(单位:辆) | 物质重量(单位:吨) | |
第一批 | 4 | 16 | 264 |
第二批 | 6 | 10 | 340 |
(1)每节火车皮和每辆汽车平均各能装多少吨物资?
(2)已知火车皮的装运费为30元吨,汽车的装运费为100元/吨.若第三批救灾物资需要5节火车皮和15辆汽车正好装完,共需要装运费多少元?