题目内容
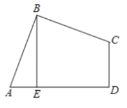
【题目】如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为144,则BE________
【答案】12
【解析】
作BF⊥CD交CD的延长线于点F,由已知条件可证得∠ABE=∠CBF,且由已知∠AEB=∠CFB=90°,AB=BC,所以△ABE≌△CBF,可得BE=BF,四边形ABCD的面积等于新正方形FBED的面积,即可得BE长.
过B点作BF⊥CD,与DC的延长线交于F点,则∠F=90°,

∵BE⊥AD,∴∠AEB=∠BED=90°,
又∵∠CDA=90°,
∴四边形BEDF是矩形,
∴∠EBF=90°,
∵∠ABC=90°,
∴∠ABE+∠EBC=∠CBF+∠EBC,
∴∠ABE=∠CBF,
又AB=BC,
∴△ABE≌△CBF,
∴BE=BF,
∴矩形BEDF为正方形,
∴S正方形BEDF=S△BCF+S四边形BEDC= S△BAE+S四边形BEDC=S四边形ABCD=144,
∴BE2=144,
∴BE=12,
故答案为:12.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目