题目内容
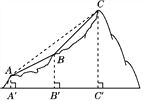
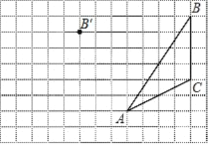
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)在给定方格纸中画出平移后的△A′B′C′;
(2)画出AB边上的中线CD
(3)画出BC边上的高线AE
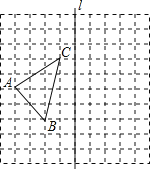
(4)点![]() 为方格纸上的格点(异于点
为方格纸上的格点(异于点![]() ),若
),若![]() ,则图中的格点
,则图中的格点![]() 共有 个.
共有 个.
【答案】(1)作图见解析;(2)作图见解析;(3)作图见解析;(4)7.
【解析】
(1)根据图形平移的性质画出平移后的△A′B′C′即可;
(2)画出AB边上的中线CD即可;
(3)过点A向BC的延长线作垂线,垂足为点E即可;
(4)过点B作BF∥AC,直线BF与格点的交点即为所求,还有AC下方的一个点.
(1)如图,△A′B′C′即为所求;
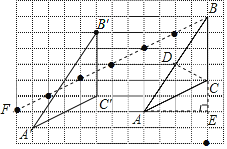
(2)如图,线段CD即为所求;
(3)如图,线段AE即为所求;
(4)如图,共有7个格点.
故答案为:7.

练习册系列答案
相关题目