题目内容
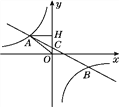
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=![]() ,点B的坐标为(m,-2).
,点B的坐标为(m,-2).
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
【答案】(1)△AHO的周长为12;(2) 反比例函数的解析式为y=![]() ,一次函数的解析式为y=-
,一次函数的解析式为y=-![]() x+1.
x+1.
【解析】试题分析: (1)根据正切函数,可得AH的长,根据勾股定理,可得AO的长,根据三角形的周长,可得答案;
(2)根据待定系数法,可得函数解析式.
试题解析:(1)由OH=3,tan∠AOH=![]() ,得
,得
AH=4.即A(-4,3).
由勾股定理,得
AO=![]() =5,
=5,
△AHO的周长=AO+AH+OH=3+4+5=12;
(2)将A点坐标代入y=![]() (k≠0),得
(k≠0),得
k=-4×3=-12,
反比例函数的解析式为y=![]() ;
;
当y=-2时,-2=![]() ,解得x=6,即B(6,-2).
,解得x=6,即B(6,-2).
将A、B点坐标代入y=ax+b,得
![]() ,
,
解得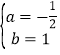 ,
,
一次函数的解析式为y=-![]() x+1.
x+1.
考点:反比例函数与一次函数的交点问题.
【题型】解答题
【结束】
23
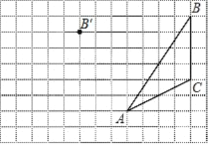
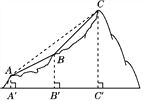
【题目】如图,点A,B,C表示某旅游景区三个缆车站的位置,线段AB,BC表示连接缆车站的钢缆,已知A,B,C三点在同一铅直平面内,它们的海拔高度AA′,BB′,CC′分别为110米,310米,710米,钢缆AB的坡度i1=1∶2,钢缆BC的坡度i2=1∶1,景区因改造缆车线路,需要从A到C直线架设一条钢缆,那么钢缆AC的长度是多少米?(注:坡度i是指坡面的铅直高度与水平宽度的比)
【答案】钢缆AC的长度为1 000米.
【解析】试题分析:过点A作AE⊥CC′于点E,交BB′于点F,过点B作BD⊥CC′于点D,分别求出AE、CE,利用勾股定理求解AC即可.
试题解析:过点A作AE⊥CC′于点E,交BB′于点F,过点B作BD⊥CC′于点D,
则△AFB、△BDC、△AEC都是直角三角形,四边形AA′B′F,BB′C′D和BFED都是矩形,
∴BF=BB′-B′F=BB′-AA′=310-110=200,
CD=CC′-C′D=CC′-BB′=710-310=400,
∵i1=1:2,i2=1:1,
∴AF=2BF=400,BD=CD=400,
又∵EF=BD=400,DE=BF=200,
∴AE=AF+EF=800,CE=CD+DE=600,
∴在Rt△AEC中,AC=![]() (米).
(米).
答:钢缆AC的长度是1000米.