题目内容
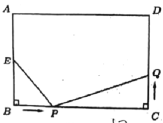
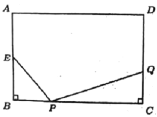
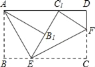
【题目】将矩形纸片ABCD按如图所示的方式折叠，AE、EF为折痕，∠BAE＝30°，BE＝1，折叠后，点C落在AD边上的C1处，并且点B落在EC1边上的B1处．则EC的长为（ ）
A. 
B. 2 C. 3 D. 2
【答案】B
【解析】
根据直角三角形30°角所对的直角边等于斜边的一半求出AE＝2，再根据直角三角形两锐角互余求出∠AEB＝60°，根据翻折变换的性质可得∠AEB1＝∠AEB，根据两直线平行，内错角相等可得∠EAC1＝∠AEB1＝60°，然后判断出△AEC1是等边三角形，根据等边三角形的性质可得BC1＝AE，再根据翻折变换的性质可得EC＝BC1．
解：∵矩形纸片ABCD，∠BAE＝30°，
∴AE＝2BE＝2×1＝2，
∠AEB＝90°﹣∠BAE＝90°﹣30°＝60°，
∵AB沿AE翻折点B落在EC1边上的B1处，
∴∠AEB1＝∠AEB＝60°，
∵矩形对边AD∥BC，
∴∠EAC1＝∠AEB1＝60°，
∴△AEC1是等边三角形，
∴BC1＝AE＝2，
∵EC沿BF翻折点C落在AD边上的C1处，
∴EC＝BC1＝2．
故选：B．
练习册系列答案
相关题目
【题目】养成良好的早锻炼习惯，对学生的学习和生活非常有益
某中学为了了解七年级学生的早锻炼情况，校政教处在七年级随机抽取了部分学生，并对这些学生通常情况下一天的早锻炼时间
分钟
进行了调查现把调查结果分为A，B，C，D四组，如下表所示；同时，将调查结果绘制成下面两幅不完整的统计图．
组别 | 早锻炼时间 |
A |
|
B |
|
C |
|
D |
|
请根据以上提供的信息，解答下列问题：
扇形统计图中D所在扇形的圆心角度数为______；
补全频数分布直方图；
已知该校七年级共有1200名学生，请你估计这个年级学生中有多少人一天早锻炼的时间不少于20分钟．
