题目内容
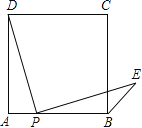
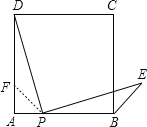
【题目】点P是正方形ABCD边AB上一点(不与A,B重合),连接PD并将线段PD绕点P顺时针旋转90°,得到线段PE,连接BE,则∠CBE等于 .
【答案】45°
【解析】
试题在AD上取一点F,使DF=BP,连接PF,由正方形的性质就可以得出△DFP≌△PBE,就可以得出∠DFP=∠PBE,根据AP=AF就可以得出∠DFP的值,就可以求出∠CBE的值.
解:在AD上取一点F,使DF=BP,连接PF,
∵四边形ABCD是正方形,
∴AD=AB,∠A=∠ABC=90°.
∴AD﹣DF=AB﹣BP,∠ADP+∠APD=90°,
∴AF=AP.
∴∠AFP=∠APF=45°,
∴∠DFP=135°.
∵∠DPE=90°
∴∠APD+∠BPE=90°.
∴∠ADP=∠BPE.
在△DFP和△PBE中,
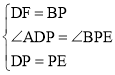 ,
,
∴△DFP≌△PBE(SAS),
∴∠DFP=∠PBE,
∴∠PBE=135°,
∴∠EBC=135°﹣90°=45°.
故答案为:45°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目