题目内容
【题目】如果一个自然数从高位到个位是由一个数字或几个数字重复出现组成的,那么我们把这样的自然数叫做循环数,重复的一个或几个数字称为“循环节”,我们把“循环节”的数字个数叫做循环节的阶数.例如:525252,它由“52”依次重复出现组成,所以525252是循环数,它是2阶6位循环数.再如:77,是1阶2位循环数,135135135是3阶9位循环数.
(1)请直接写出1个2阶4位循环数 ,并证明对于任意一个2阶4位循环数,若交换其循环节的数字得到一个新的4位数,则该新数和原数的差能够被9整除.
(2)已知一个能被9整除的2阶4位数.设循环节为ab,且满足a﹣2b为非负偶数,求这个4位循环数.
【答案】(1)7171,证明见解析;(2)这个4位循环数为6363或8181.
【解析】
(1)根据循环节”的数字个数叫做循环节的阶数,可得答案;
(2)根据一个能被9整除的2阶4位循环数,可得![]() 能被9整除,即(a+b)能被9整除,得到a+b=9或a+b=18,根据a﹣2b为非负偶数,分类讨论可得答案.
能被9整除,即(a+b)能被9整除,得到a+b=9或a+b=18,根据a﹣2b为非负偶数,分类讨论可得答案.
(1)7171是2阶4位循环数;
证明:设原数为![]() ,新数为
,新数为![]() 即原数1000a+100b+10a+b,新数是1000b+100a+10b+a,
即原数1000a+100b+10a+b,新数是1000b+100a+10b+a,
1000b+100a+10b+a﹣(1000a+100b+10a+b)
=909b﹣909a
=909(b﹣a)
=9×101(b﹣a).
∵a,b为整数,
∴b﹣a也为整数,
∴新数和原数的差能够被9整除.
故答案为:7171.
(2)该2阶4位循环数为![]() ,
,
即![]() 112a+11b
112a+11b![]() ,
,
要使得1010a+101b能被9整除,则需(a+b)能被9整除.
∵0<a≤9,0<b≤9,
∴0<a+b≤18,
∴a,b应满足的关系是a+b=9或a+b=18.
①当a+b=9,即a=9-b时,
又∵a﹣2b为非负偶数,
∴9-b-2b≥0,
∴b≤3.
∵b为正整数,
∴b=1,2,3.
当b=1时,a=8,a-2b=8-2=6是非负偶数,满足条件;
当b=2时,a=7,a-2b=7-4=3不是非负偶数,不满足条件;
当b=3时,a=6,a-2b=6-6=0是非负偶数,满足条件;
∴这个4位循环数为8181或6363.
②当a+b=18,即a=18-b时,a=b=9,此时a-2b=-9不是非负偶数,不满足条件.
综上所述:这个4位循环数为6363或8181.

【题目】某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查,将他们的得分按优秀、良好、合格、不合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.
等级 | 频数 | 频率 |
优秀 | 20 |
|
良好 | ||
合格 | 10 |
|
不合格 | 5 |
|
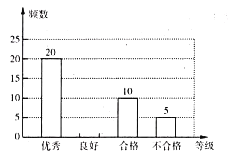
请根据以上信息,解答下列问题:
(1)本次调查随机抽取了______名学生;表中![]() ______,
______,![]() ______;
______;
(2)补全条形统计图;
(3)若全校有2000名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.