Question

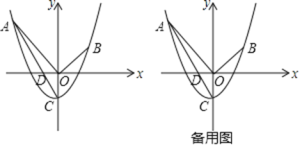
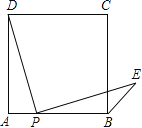
【题目】点P到图形Ω（可以是线段、三角形、圆或不规则图形等）的距离是指:点P与图形Ω中所有点连接的线段中最短线段的长度.如图①中的两个虚线段PQ的长度都表示点P到图形Ω的距离.

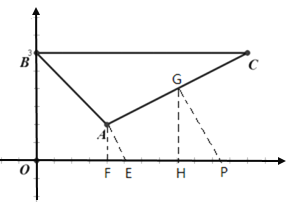
如图②，在平面直角坐标系xOy中，△ABC的三个顶点坐标分别为，点P从原点出发，以每秒1个单位长度的速度向x轴的正方向运动了t秒.

（1）当t=0时，求点P到△ABC的距离；

（2）当点P到△ABC的距离等于线段AP的长度时，求t的范围；

（3）当点P到△ABC的距离大于时，求t的取值范围.

Answer 1

【答案】（1）；（2）当时，P到△ABC的距离等于线段PA的长度；（3）当t>5时，点P到△ABC的距离大于

【解析】

（1）作AM⊥BC，ON⊥AB，根据A、B、C三点的坐标求出△AMB为等腰直角三角形，继而求出∠OBN=45°，即可得到ON的长度；

（2）过点A分别作AB与AC的垂线，与x轴分别交于点D、E，当P运动到D、E之间时，P到△ABC的距离等于PA的长度，求得AD、AE的长度即可得到取值范围；

（3）由（1）可知P点只能在E点右侧，作PG⊥AC，作GH⊥x轴，利用三角形相似求出G点的横坐标为4，且HP=2FE=1，由此求出t的取值范围.

（1）作AM⊥BC，ON⊥AB，

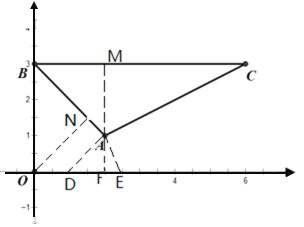
由得BC∥x轴，

∴AM=BM=2

∴△AMB为等腰直角三角形，∠ABM=45°

∴∠OBN=45°

∴

（2）作AF⊥x轴，过点A分别作AB与AC的垂线，与x轴分别交于点D、E

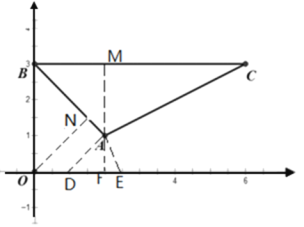
当P运动到D、E之间时，P到△ABC的距离等于PA的长度

△ADF中，∠ADF=45° DF=AF=1，故点D横坐标为1

∵△AFE~△CMA

∴

∴FE=，故点E的横坐标为

∴当时，P到△ABC的距离等于线段PA的长度

（3）直线AC的方程为

∵，P点只能在E点右侧，

作PG⊥AC，作GH⊥x轴

△AFE~△GHP

故GH=2，又直线AC的方程为

当y=2时， 得x=4，

∴G点的横坐标为4，且HP=2FE=1

故点P的横坐标为5

当t>5时，点P到△ABC的距离大于