题目内容
【题目】直线![]() 与x轴交于点A,与y轴交于点B.点C是x轴上一动点,点D为(3,0),抛物线
与x轴交于点A,与y轴交于点B.点C是x轴上一动点,点D为(3,0),抛物线![]() 过B、C、D三点.
过B、C、D三点.
(1)如图1所示,若点C与点A关于y轴对称.
①求直线BD和抛物线的解析式;
②若点P是抛物线对称轴上一动点,当BP+CP的值最小时,求点P的坐标;
③若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标;
(2)如图2,若BE//x轴,且E(4,3),点A1与点A关于直线BC对称,当EA1的长最小时,直接写出OC的长.


【答案】(1)①y=x2﹣4x+3.②点P(2,1).③(0,0),(﹣3,0)或(0,﹣3).(2) OC=![]() .
.
【解析】试题分析:(1)①由直线y=3x+3可得A、B点的坐标,再根据A、C关于y轴对称得到点C坐标,然后利用待定系数法即可得直线与抛物线的解析式;
②BD与对称轴的交点即为所求作的点;
③分情况讨论即可得;
(2)根据题意可知当点A1落在BE上时,EA1最小,由此即可得.
试题解析:(1)①∵直线l:y=3x+3与x轴交于点A,与y轴交于点B,
∴A(﹣1,0),B(0,3),
∵点A与点C关于y轴对称,
∴C(1,0),
设直线BD的解析式为:y=kx+b,
∵点B(0,3),D(3,0)在直线BD上,
∴![]() ,解得k=﹣1,b=3,
,解得k=﹣1,b=3,
∴直线BD的解析式为:y=﹣x+3;
设抛物线的解析式为:y=a(x﹣1)(x﹣3),
∵点B(0,3)在抛物线上,
∴3=a×(﹣1)×(﹣3),
解得:a=1,
∴抛物线的解析式为:y=(x﹣1)(x﹣3)=x2﹣4x+3;
②点C关于对称轴的对称点为D,
直线BD的解析式为:y=﹣x+3,
当x=2时,y=1,
∴点P(2,1);
③抛物线的解析式为:y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的对称轴为直线x=2,顶点坐标为(2,﹣1),
直线BD:y=﹣x+3与抛物线的对称轴交于点M,令x=2,得y=1,
∴M(2,1),
设对称轴与x轴交点为点F,则CF=FD=MF=1,
∴△MCD为等腰直角三角形,
∵以点N、B、D为顶点的三角形与△MCD相似,
∴△BND为等腰直角三角形,
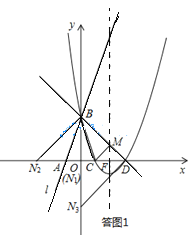
如答图1所示:
(I)若BD为斜边,则易知此时直角顶点为原点O,
∴N1(0,0);
(II)若BD为直角边,B为直角顶点,则点N在x轴负半轴上,
∵OB=OD=ON2=3,
∴N2(﹣3,0);
(III)若BD为直角边,D为直角顶点,则点N在y轴负半轴上,
∵OB=OD=ON3=3,
∴N3(0,﹣3),
∴满足条件的点N坐标为:(0,0),(﹣3,0)或(0,﹣3);
(2)如图所示,当点A1在BE上是时,EA1最小,
由OB=3,OA=1,根据勾股定理可得AB=![]() ,所以BA1=BA=
,所以BA1=BA=![]() ,
,
易证明四边形ACA1B是菱形,所以AC=AB=![]() ,所以OC=
,所以OC=![]() -1.
-1.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案