��Ŀ����
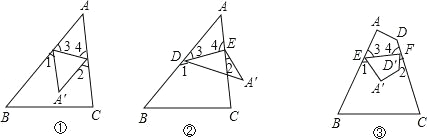
����Ŀ����1����ͼ�٣��ѡ�ABC ֽƬ�� DE �۵���ʹ�� A �����ı��� BCED ���ڲ��� A����λ�ã���˵�� 2��A=��1+��2��
��2����ͼ�ڣ����ѡ�ABC ֽƬ�� DE �۵���ʹ�� A �����ı��� BCED ���ⲿ��A���λ�ã�д����A ���1����2 ֮��ĵ�����ϵ������˵����������
��3����ͼ�ۣ������ı��� ABCD �� EF �۵���ʹ�� A��D �����ı���BCFE ���ڲ��� A�䡢D���λ�ã�����̽����ʱ��A����D����1 ���2 ֮���������ϵ��д���㷢�ֵĽ��۲�˵�����ɣ�

���𰸡���1��˵������������2��2��A=��1����2����3��2����A+��D��=��1+��2+360��. ���ɼ�����.
��������
��1�����ݷ��۵����ʱ�ʾ����3����4���ٸ��������ε��ڽǺͶ�����ʽ�������ɵý⣻
��2���ȸ��ݷ��۵������Լ�ƽ�ǵĶ����ʾ����3����4���ٸ��������ε��ڽǺͶ�����ʽ�������ɵý⣻
��3���ȸ��ݷ��۵����ʱ�ʾ����3����4���ٸ����ı��ε��ڽǺͶ�����ʽ�������ɵý⣮
��1����ͼ�����ݷ��۵����ʣ�
��3=![]() ��180����1������4=
��180����1������4=![]() ��180����2����
��180����2����
�ߡ�A+��3+��4=180�㣬
���A+![]() ��180����1��+
��180����1��+![]() ��180����2��=180�㣬
��180����2��=180�㣬
�����ã�2��A=��1+��2��
��2�����ݷ��۵����ʣ���3=![]() ��180����1������4=
��180����1������4=![]() ��180+��2����
��180+��2����
�ߡ�A+��3+��4=180�㣬
���A+ ![]() ��180����1��+
��180����1��+ ![]() ��180+��2��=180�㣬
��180+��2��=180�㣬
�����ã�2��A=��1����2��
��3�����ݷ��۵����ʣ���3=![]() ��180����1������4=
��180����1������4=![]() ��180����2����
��180����2����
�ߡ�A+��D+��3+��4=360�㣬
���A+��D+ ![]() ��180����1��+
��180����1��+ ![]() ��180����2��=360�㣬
��180����2��=360�㣬
�����ã�2����A+��D��=��1+��2+360�㣮

 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�����Ŀ��Ϊ�˴Ӽס�������ѡ����ѡ��һ���μ�����������ֶ����ǽ���һ�β��飬����������ͬ�����¸����10�Σ�Ϊ�˱Ƚ����˵ijɼ�������������ͳ��ͼ���� �ס�������ɼ�ͳ�Ʊ�
ƽ���� | ��λ�� | ���� | ����10���Ĵ��� | |
�� | 7 | 0 | ||
�� | 1 |
�ס�������ɼ�����ͼ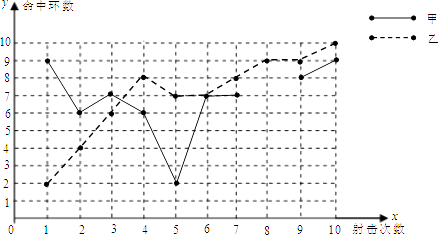
��1���벹ȫ����ͼ������ֱ���ڱ�����պͲ�ȫ����ͼ����
��2������涨�ɼ����ȶ���ʤ��������Ϊ˭Ӧʤ����˵��������ɣ�
��3�����ϣ����2���е���һ��ѡ��ʤ��������ͼ���е���Ϣ��Ӧ���ƶ����������й���Ϊʲô��