题目内容
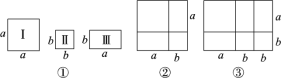
【题目】嘉嘉同学动手剪了如图①所示的正方形与长方形纸片若干张.
问题发现
(1)他用1张Ⅰ型、1张Ⅱ型和2张Ⅲ型卡片拼出一个新的图形(如图②).根据图形的面积关系写出一个你所熟悉的乘法公式,这个乘法公式是________________;
(2)如果要拼成一个长为a+2b,宽为a+b的大长方形,那么需要Ⅱ型卡片________张,Ⅲ型卡片________张.
拓展探究
(3)若a+b=5,ab=6,求a2+b2的值;
(4)当他拼成如图③所示的长方形时,根据图形的面积,可把多项式a2+3ab+2b2分解因式,其结果是________.
解决问题
(5)请你依照嘉嘉的方法,利用拼图分解因式:a2+5ab+6b2=________.
【答案】(1)(a+b)2=a2+2ab+b2;(2)2,3;(3)13;(4)(a+2b)(a+b);(5)(a+2b)(a+3b)
【解析】
(1)利用图②的面积可得出这个乘法公式是(a+b)2=a2+2ab+b2;
(2)由如图③可得要拼成一个长为(a+2b),宽为(a+b)的大长方形所需要的Ⅱ型卡片、Ⅲ型卡片的数量;
(3)根据a2+b2= (a+b)2-2ab计算即可;
(4)由图③可知矩形面积为(a+2b)(a+b),利用面积得出a2+3ab+2b2=(a+2b)(a+b);
(5)先分解因式,再根据边长画图即可.
(1)这个乘法公式是(a+b)2=a2+2ab+b2.
故答案为:(a+b)2=a2+2ab+b2.
(2)由如图③可得要拼成一个长为(a+2b),宽为(a+b)的大长方形,则需要2号卡片2张,3号卡片3张.
故答案为:2,3.
(3)a2+b2= (a+b)2-2ab=25-2×6=25-12=13.
(4)由图③可知矩形面积为(a+2b)(a+b),所以a2+3ab+2b2=(a+2b)(a+b).
故答案为:(a+2b)(a+b).
(5)a2+5ab+6b2=(a+2b)(a+3b),如图:

故答案为:(a+2b)(a+3b).

【题目】某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路.如果平均每天的修建费y(万元)与修建天数x(天)之间在30≤x≤120,具有一次函数的关系,如下表所示.
X | 50 | 60 | 90 | 120 |
y | 40 | 38 | 32 | 26 |
(1)求y关于x的函数解析式;
(2)后来在修建的过程中计划发生改变,政府决定多修2千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了15天,求原计划每天的修建费.