题目内容
【题目】为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表: 甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | 0 | ||
乙 | 1 |
甲、乙射击成绩折线图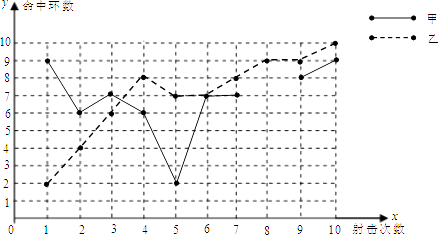
(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
【答案】
(1)解:根据折线统计图得:
乙的射击成绩为:2,4,6,8,7,7,8,9,9,10,
则平均数为 ![]() =7(环),中位数为7.5(环),
=7(环),中位数为7.5(环),
方差为 ![]() [(2﹣7)2+(4﹣7)2+(6﹣7)2+(8﹣7)2+(7﹣7)2+(7﹣7)2+(8﹣7)2+(9﹣7)2+(9﹣7)2+(10﹣7)2]=5.4;
[(2﹣7)2+(4﹣7)2+(6﹣7)2+(8﹣7)2+(7﹣7)2+(7﹣7)2+(8﹣7)2+(9﹣7)2+(9﹣7)2+(10﹣7)2]=5.4;
甲的射击成绩为9,6,7,6,2,7,7,?,8,9,平均数为7(环),
则甲第八环成绩为70﹣(9+6+7+6+2+7+7+8+9)=9(环),
所以甲的10次成绩为:9,6,7,6,2,7,7,9,8,9.
中位数为7(环),
方差为 ![]() [(9﹣7)2+(6﹣7)2+(7﹣7)2+(6﹣7)2+(2﹣7)2+(7﹣7)2+(7﹣7)2+(9﹣7)2+(8﹣7)2+(9﹣7)2]=4.
[(9﹣7)2+(6﹣7)2+(7﹣7)2+(6﹣7)2+(2﹣7)2+(7﹣7)2+(7﹣7)2+(9﹣7)2+(8﹣7)2+(9﹣7)2]=4.
补全表格如下:
甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | 7 | 4 | 0 |
乙 | 7 | 7.5 | 5.4 | 1 |
甲、乙射击成绩折线图
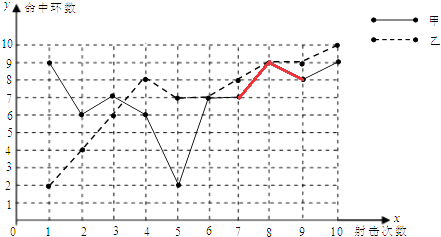
(2)解:由甲的方差小于乙的方差,甲比较稳定,故甲胜出
(3)解:如果希望乙胜出,应该制定的评判规则为:平均成绩高的胜出;如果平均成绩相同,则随着比赛的进行,发挥越来越好者或命中满环(10环)次数多者胜出.因为甲乙的平均成绩相同,乙只有第5次射击比第四次射击少命中1环,且命中1次10环,而甲第2次比第1次、第4次比第3次,第5次比第4次命中环数都低,且命中10环的次数为0次,即随着比赛的进行,有可能乙的射击成绩越来越好
【解析】(1)根据折线统计图列举出乙的成绩,计算出甲的中位数,方差,以及乙平均数,中位数及方差,补全即可;(2)计算出甲乙两人的方差,比较大小即可做出判断;(3)希望甲胜出,规则改为9环与10环的总数大的胜出,因为甲9环与10环的总数为4环.
【考点精析】通过灵活运用统计表和折线统计图,掌握制作统计表的步骤:(1)收集整理数据.(2)确定统计表的格式和栏目数量,根据纸张大小制成表格.(3)填写栏目、各项目名称及数据.(4)计算总计和合计并填入表中,一般总计放在横栏最左格,合计放在竖栏最上格.(5)写好表格名称并标明制表时间;能清楚地反映事物的变化情况,但是不能清楚地表示出在总体中所占的百分比即可以解答此题.

【题目】“中国梦”关乎每个人的幸福生活,为进一步感知我们身边的幸福,展现成都人追梦的风采,我市某校开展了以“梦想中国,逐梦成都”为主题的摄影大赛,要求参赛学生每人交一件作品.现将参赛的50件作品的成绩(单位:分)进行统计如下:
等级 | 成绩(用s表示) | 频数 | 频率 |
A | 90≤s≤100 | x | 0.08 |
B | 80≤s<90 | 35 | y |
C | s<80 | 11 | 0.22 |
合 计 | 50 | 1 |
请根据上表提供的信息,解答下列问题:
(1)表中的x的值为 , y的值为
(2)将本次参赛作品获得A等级的学生依次用A1 , A2 , A3 , …表示,现该校决定从本次参赛作品中获得A等级学生中,随机抽取两名学生谈谈他们的参赛体会,请用树状图或列表法求恰好抽到学生A1和A2的概率.