题目内容
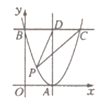
【题目】如图，在平面直角坐标系中，抛物线y=(x-2)2与x轴交于点A，与y轴交于点B，过点B作BC∥x轴，交抛物线于点C，过点A作AD∥y轴，交BC于点D，点P在BC下方的抛物线上(不与点B，C重合)，连接PC，PD，设△PCD的面积为S，则S的最大值是________。
【答案】4
【解析】
根据抛物线的解析式求得A、B的坐标，和对称轴方程，根据BC∥x轴，AD∥y轴对称B、C是抛物线上的对称点，所以BD=DC=2，因为顶点A到直线BC的距离最大，所以点P与A重合时，△PCD面积最大，最大值为
DCAD=×2×4=4．
∵抛物线y=(x2)2与x轴交于点A，与y轴交于点B.
∴A(2,0),B(0,4)，
∵抛物线y=(x2)2与的对称轴为x=2,BC∥x轴,AD∥y轴，
∴直线AD就是抛物线y=(x2)2与的对称轴，
∴B、C关于直线BD对称，
∴BD=DC=2，
∵顶点A到直线BC的距离最大，
∴点P与A重合时,△PCD面积最大,最大值为DCAD=×2×4=4.
故最大值为4.
练习册系列答案
相关题目
【题目】下列表格是某学校女子排球队队员年龄统计表：
年龄（岁） | 13 | 14 | 15 | 16 |
人数（人） | 1 | 2 | 4 | 5 |
（1）该排球队队员年龄的众数是 岁；
（2）事件“从该排球队随机选择一名队员，其年龄为13岁”发生的概率为 ；
（3）教练決定从年龄为13岁和14岁的A、B、C三名队员中，随机选取两名队员进行“接发球”训练，求队员A、B同时被选中的概率．（树状图或列表法）
