Question

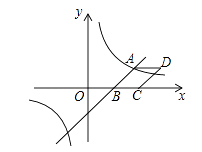
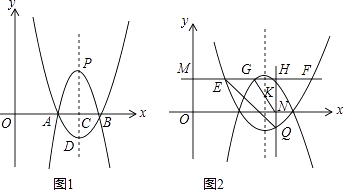
【题目】如图1，二次函数y1=（x﹣2）（x﹣4）的图象与x轴交于A、B两点（点A在点B的左侧），其对称轴l与x轴交于点C，它的顶点为点D．

（1）写出点D的坐标 ．
（2）点P在对称轴l上，位于点C上方，且CP=2CD，以P为顶点的二次函数y2=ax2+bx+c（a≠0）的图象过点A．
试说明二次函数y2=ax2+bx+c（a≠0）的图象过点B；
（3）点R在二次函数y1=（x﹣2）（x﹣4）的图象上，到x轴的距离为d，当点R的坐标为时，二次函数y2=ax2+bx+c（a≠0）的图象上有且只有三个点到x轴的距离等于2d；
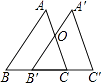
（4）如图2，已知0＜m＜2，过点M（0，m）作x轴的平行线，分别交二次函数y1=（x﹣2）（x﹣4）、y2=ax2+bx+c（a≠0）的图象于点E、F、G、H（点E、G在对称轴l左侧），过点H作x轴的垂线，垂足为点N，交二次函数y1=（x﹣2）（x﹣4）的图象于点Q，若△GHN∽△EHQ，求实数m的值．

Answer 1

【答案】
（1）（3，﹣1）
（2）

解：∵点P在对称轴l上，位于点C上方，且CP=2CD，

∴点P的坐标为（3，2），

∴二次函数y1=（x﹣2）（x﹣4）与y2=ax2+bx+c的图象的对称轴均为x=3，

∵点A、B关于直线x=3对称，

∴二次函数y2=ax2+bx+c（a≠0）的图象过点B

（3）解：（3﹣ ，1）、（3+ ，1）或（3，﹣1）
（4）

解：（方法一）设过点M平行x轴的直线交对称轴l于点K，直线l也是二次函数y2=ax2+bx+c（a≠0）的图象的对称轴．

∵二次函数y2=ax2+bx+c过点A、B，且顶点坐标为P（3，2），

∴二次函数y2=﹣2（x﹣2）（x﹣4）．

设N（n，0），则H（n，﹣2（n﹣2）（n﹣4）），Q（n，（n﹣2）（n﹣4）），

∴HN=2（n﹣2）（n﹣4），QN=（n﹣2）（n﹣4），

∴ =2，即 = ．

∵△GHN∽△EHQ，

∴ ．

∵G、H关于直线l对称，

∴KG=KH= HG，

∴ ．

设KG=t（t＞0），则G的坐标为（3﹣t，m），E的坐标为（3﹣2t，m），

由题意得： ，

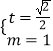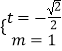解得： 或 （舍去）．

故当△GHN∽△EHQ，实数m的值为1．

（方法二）令y1=x2﹣6x+8=m，

解得：x=3± ，

∴点E（3﹣ ，m）．

∵二次函数y2=ax2+bx+c过点A、B，且顶点坐标为P（3，2），

∴二次函数y2=﹣2（x﹣2）（x﹣4）．

令y2=﹣2（x﹣2）（x﹣4）=﹣2x2+12x﹣16=m，

解得：x=3± ，

∴点G（3﹣ ，m），点H（3+ ，m）．

当x=3+ 时，y1=（x﹣2）（x﹣4）=（1+ ）（ ﹣1）=﹣ m，

∴点Q（3+ ，﹣ m）．

HG=xH﹣xG= ，HE=xH﹣xE= + ，HN=yH﹣yN=m，HQ=yH﹣yQ= m，

∵△GHN∽△EHQ，

∴ = = ，

整理得：4﹣2m=m+1，

解得：m=1，

将检验后可得m=1是方程 = 的解．

故当△GHN∽△EHQ，实数m的值为1．

【解析】解：（1）∵y1=（x﹣2）（x﹣4）=x2﹣6x+8=（x﹣3）2﹣1，
∴顶点D的坐标为（3，﹣1）．
故答案为：（3，﹣1）．（3）∵二次函数y2=ax2+bx+c的顶点坐标P（3，2），且图象上有且只有三个点到x轴的距离等于2d，
∴2d=2，解得：d=1．
令y1=（x﹣2）（x﹣4）=x2﹣6x+8中y1=±1，即x2﹣6x+8=±1，
解得：x1=3﹣ ，x2=3+ ，x3=3，
∴点R的坐标为（3﹣ ，1）、（3+ ，1）或（3，﹣1）．
故答案为：（3﹣ ，1）、（3+ ，1）或（3，﹣1）．
（1）利用配方法将二次函数y1=（x﹣2）（x﹣4）变形为顶点式，由此即可得出结论；（2）由点P在对称轴l上，可得出二次函数y2=ax2+bx+c的图象的对称轴为直线l，再结合点A、B关于对称轴l对称，二次函数y2=ax2+bx+c（a≠0）的图象过点A，即可得出二次函数y2=ax2+bx+c（a≠0）的图象过点B；（3）由二次函数y2=ax2+bx+c（a≠0）的图象上有且只有三个点到x轴的距离等于2d，即可得出d=1，再令二次函数y1=（x﹣2）（x﹣4）中y1=±1求出x值，即可得出结论；（4）（方法一）设N（n，0），则H（n，﹣2（n﹣2）（n﹣4）），Q（n，（n﹣2）（n﹣4）），由此即可得出 = ，根据相似三角形的性质即可得出 ，再根据对称性可得出 ，设KG=t（t＞0），则G的坐标为（3﹣t，m），E的坐标为（3﹣2t，m），由此即可得出关于m、t的二元一次方程组，解方程组即可求出m值；（方法二）将y=m分别代入y1、y2中求出点E、G、H的坐标，再将点H的横坐标代入y1中可得出点N的坐标，由此即可得出HG、HE、HN、HQ的长度，根据相似三角形的性质即可得出关于m的无理方程，解之经检验后即可得出结论．