��Ŀ����
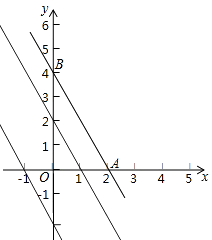
����Ŀ���������һ�κ���y=k1x+b1��y=k2x+b2����k1=k2 �� b1��b2 �� ��ô��������һ�κ���Ϊ��ƽ��һ�κ������� ��ͼ����֪����y=��2x+4��ͼ����x�ᡢy��ֱ���A��B���㣬һ�κ���y=kx+b��y=��2x+4�ǡ�ƽ��һ�κ�����
��1��������y=kx+b��ͼ����㣨3��1������b��ֵ��
��2��������y=kx+b��ͼ������������Χ�ɵ������κ͡�AOB����λ��ͼ�Σ�λ������Ϊԭ�㣬λ�Ʊ�Ϊ1��2������y=kx+b�ı���ʽ��
���𰸡�
��1���⣺����֪�ã�k=��2��
�ѵ㣨3��1����k=��2����y=kx+b�еã�1=��2��3+b��
��b=7
��2���⣺����λ�Ʊ�Ϊ1��2�ã�����y=kx+b��ͼ�������������
�ٲ�������������ʱ������1��0���ͣ�0��2������ʱ����ʾΪ��y=��2x+2��
�ڲ�������һ����ʱ��������1��0���ͣ�0����2������ʱ����ʾΪ��y=��2x��2��
����������1������ƽ��һ�κ����Ķ����֪��k=��2�������ô���ϵ�������b��ֵ���ɣ���2������λ�Ʊ�Ϊ1��2��֪������y=kx+b��������Ľ������꣬�����ô���ϵ�����������y=kx+b�ı���ʽ��

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��ijУΪ�˽�ȫУѧ����ѧ�ڲμ�������������ѧУ��������˱�У50��ѧ���μ�������Ĵ����������������õ������������£� �μ������������Ƶ����Ƶ�ʷֲ���
�����x | Ƶ�� | Ƶ�� |
0��x��3 | 10 | 0.20 |
3��x��6 | a | 0.24 |
6��x��9 | 16 | 0.32 |
9��x��12 | 6 | 0.12 |
12��x��15 | m | b |
15��x��18 | 2 | n |
��������ͼ����Ϣ������������⣺
��1������a= �� b=��
��2�����Ƶ���ֲ�ֱ��ͼ������������ͼ�����ע��Ӧ�����ݣ���
��3������У����1200��ѧ��������Ƹ�У����ѧ�ڲμ����������6�ε�ѧ���ж����ˣ�
����Ŀ���ˣ�2������֯��һ�ξ����ʶ��������ס������Ӹ�10�˵ı����ɼ����±���10���ƣ���
�� | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
�� | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
��1���ӳɼ�����λ�����֣��Ҷӳɼ����������֣�
��2�������Ҷӵ�ƽ���ɼ��ͷ��
��3����֪�ӳɼ��ķ�����1.4��2 �� ��ɼ���Ϊ��������ӣ�



