题目内容
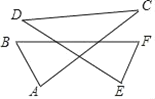
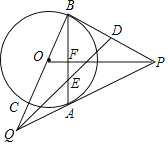
【题目】如图,P是⊙O外的一点,PA、PB是⊙O的两条切线,A、B是切点,PO交AB于点F,延长BO交⊙O于点C,交PA的延长交于点Q,连结AC.
(1)求证:AC∥PO;
(2)设D为PB的中点,QD交AB于点E,若⊙O的半径为3,CQ=2,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】(1)根据切线长定理得出PA=PB,且PO平分∠BPA,利用等腰三角形三线合一的性质得出PO⊥AB.根据圆周角定理得出AC⊥AB,进而得到AC∥PO;
(2)连结OA、DF.先用勾股定理计算出AQ=4,再计算出PA=PB=6,利用切线长定理可得到F点为AB的中点,易得DF为△BAP的中位线,则DF=![]() PA=3,DF∥PA,利用DF∥AQ得到△DFE∽△QEA,所以
PA=3,DF∥PA,利用DF∥AQ得到△DFE∽△QEA,所以![]() ,设AE=4t,FE=3t,则AF=AE+FE=7t,于是BE=BF+FE=AF+FE=7t+3t=10t,最后计算
,设AE=4t,FE=3t,则AF=AE+FE=7t,于是BE=BF+FE=AF+FE=7t+3t=10t,最后计算![]() .
.
(1)证明:∵PA、PB是⊙O的两条切线,A、B是切点,
∴PA=PB,且PO平分∠BPA,
∴PO⊥AB.
∵BC是直径,
∴∠CAB=90°,
∴AC⊥AB,
∴AC∥PO;
(2)连结OA、DF,如图,

∵PA、PB是⊙O的两条切线,A、B是切点,
∴∠OAQ=∠PBQ=90°.
在Rt△OAQ中,OA=OC=3,
∴OQ=5.
由QA2+OA2=OQ2,得QA=4.
在Rt△PBQ中,PA=PB,QB=OQ+OB=8,由QB2+PB2=PQ2,得82+PB2=(PB+4)2,解得PB=6,
∴PA=PB=6.
∵OP⊥AB,
∴BF=AF=![]() AB.
AB.
又∵D为PB的中点,
∴DF∥AP,DF=![]() PA=3,
PA=3,
∴△DFE∽△QEA,
∴![]()
设AE=4t,FE=3t,则AF=AE+FE=7t,
∴BE=BF+FE=AF+FE=7t+3t=10t,
∴![]() .
.