题目内容
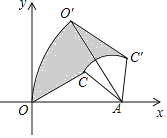
【题目】如图,△OAC的顶点O在坐标原点,OA边在x轴上,OA=2,AC=1,把△OAC绕点A按顺时针方向旋转到△O′AC′,使得点O′的坐标是(1,![]() ),则在旋转过程中线段OC扫过部分(阴影部分)的面积为______.
),则在旋转过程中线段OC扫过部分(阴影部分)的面积为______.
【答案】![]()
【解析】
过O′作O′M⊥OA于M,解直角三角形求出旋转角的度数,根据图形得出阴影部分的面积S=S扇形OAO′+S△O′AC′-S△OAC-S扇形CAC′=S扇形OAO′-S扇形CAC′,分别求出即可.
过O′作O′M⊥OA于M,则∠O′MA=90°,

∵点O′的坐标是(1,![]() ),
),
∴O′M=![]() ,OM=1,
,OM=1,
∵AO=2,
∴AM=2-1=1,
∴tan∠O′AM=![]() ,
,
∴∠O′AM=60°,
即旋转角为60°,
∴∠CAC′=∠OAO′=60°,
∵把△OAC绕点A按顺时针方向旋转到△O′AC′,
∴S△OAC=S△O′AC′,
∴阴影部分的面积S=S扇形OAO′+S△O′AC′-S△OAC-S扇形CAC′=S扇形OAO′-S扇形CAC′
=![]()
=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目