题目内容
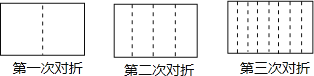
【题目】将一张长方形的纸对折，如图所示，可得到一条折痕（图中虚线），继续对折，对折时每次折痕与上次的折痕保持平行，连续对折三次后，可以得到7条折痕，
（1）折一折，数一数，连续对折四次后，可以得到多少条折痕？
（2）想一想，如果对折n次，可以得到多少条折痕？
（3）如果能对折10次，可以得到多少条折痕？
（4）如果对折n次，可以得到多少个一样大小的小长方形？
【答案】（1）15；（2）2n﹣1；（3）1023；（4）2n.
【解析】
（1）对前三次对折可经发现每对折1次把纸分成的部分是上一次的2倍，折痕数是所分成的部分数少1，据此可求出第4次的折痕；
（2）根据（1）对折规律求出对折n次得到的部分数，然后减1即可得到折痕条数；
（3）把n=10代入（2）中的式子即可计算出结果；
（4）对折n次得到的部分数就是小长方形的个数.
解：由图可知，第1次对折，把纸分成2部分，1条折痕，
第2次对折，把纸分成4部分，3条折痕，
第3次对折，把纸分成8部分，7条折痕，
（1）第4次对折，把纸分成16部分，15条折痕，
（2）依此类推，第n次对折，把纸分成2n部分，2n﹣1条折痕．
（3）第10次对折，把纸分成210部分，210﹣1＝1023条折痕；
（4）对折n次，可以得到2n个一样大小的小长方形
练习册系列答案
同步练习强化拓展系列答案
相关题目
