题目内容
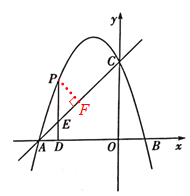
【题目】如图,抛物线![]() 与两轴分别交于A、B、C三点,已知点A(一3,O),B(1,0).点P在第二象限内的抛物线上运动,作PD上
与两轴分别交于A、B、C三点,已知点A(一3,O),B(1,0).点P在第二象限内的抛物线上运动,作PD上![]() 轴子点D,交直线AC于点E.
轴子点D,交直线AC于点E.

(1) ![]()
(2)过点P作PF⊥AC于点F.求当△PEF的周长取最大值时点P的坐标.
(3)连接AP,并以AP为边作等腰直角△APQ,当顶点Q恰好落在抛物线的对称轴上时,求对应的P点坐标.
【答案】(1) -2; 3 ;(2)( ![]() ,
, ![]() )(3)
)(3) 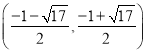 ,
, ![]()
【解析】试题分析:(1)将A、B两点坐标代入解析式中即可求出b、c的值;
(2)通过点P、E的坐标可求出PE=![]() ,由题可知,△PEF为等腰直角三角形,当PE最大时,此三角形的周长最大,求出令PE最大的x值,即可求出P点的坐标;
,由题可知,△PEF为等腰直角三角形,当PE最大时,此三角形的周长最大,求出令PE最大的x值,即可求出P点的坐标;
(3)对以P、Q、A三个顶点的角分别为直角时所形成的等腰直角三角形进行分类讨论即可.
解:(1)∵A(一3,O),B(1,0)在抛物线![]() 的图象上,
的图象上,
∴![]()
解得![]()
故答案为:-2,3 ;
(2)∵C(0,3),A(-3,0)
∴AO=CO
∴∠CAO=45°
∵PD上![]() 轴于点D
轴于点D
∴∠ADE=90°
∴∠AED=45°
∵PF⊥AC于点F
且∠PEF=∠AED=45°
∴△PEF为等腰直角三角形
∴当PE最大时,此三角形的周长最大,
由C(0,3),A(-3,0)可知直线AC的解析式为
![]()
设P(x, ![]() ),则E点坐标为(x,x+3)
),则E点坐标为(x,x+3)
∴PE=![]() (-3<x<0)
(-3<x<0)
∵当![]() 时,PE最大,即此时△PEF的周长取最大值
时,PE最大,即此时△PEF的周长取最大值
∴P点坐标为(![]() ,
,![]() )
)
(3)有三种情况:
①当∠APQ=90°且PA=PQ时,P点坐标为
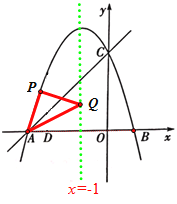
②当∠PAQ=90°且AP=AQ时,P点坐标为![]()
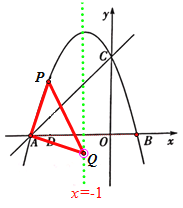
③当∠AQP=90°且PQ=AQ时,P点坐标为![]()
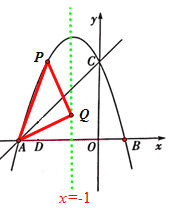
故P点坐标为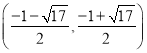 ,
, ![]()

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目