题目内容
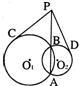3、如图，⊙O1与⊙O2相交于A、B两点，连接AB，并在其延长线上取点P，过P作⊙O1、⊙O2的切线PC、PD，切点分别为C、D，若PC=6，则PD=6
．分析：根据切割线定理得：PC2=PB•PA，PD2=PA•PB，则PC2=PD2，从而求得PD的长．
解答：解：∵依题意可得：PC2=PB•PA，PD2=PA•PB，
∴PC2=PD2，
∵PC=6，
∴PC=PD=6．
∴PC2=PD2，
∵PC=6，
∴PC=PD=6．
点评：注意：切割线定理和割线定理必须在同一个圆中运用；这里借助割线PBA建立了两条切线长的相等关系．
练习册系列答案
阅读快车系列答案
相关题目
12、已知：如图，⊙O1与⊙O2外切于点P，直线AB过点P交⊙O1于A，交⊙O2于B，点C、D分别为⊙O1、⊙O2上的点，且∠ACP=65°，则∠BDP=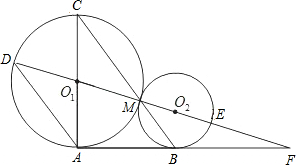
已知：如图，⊙O1与⊙O2外切于M点，AF是两圆的外公切线，A、B是切点，DF经过O1、O2，分别交⊙O1于D、⊙O2于E，AC是⊙O1的直径，BC经过M点，连接AD．
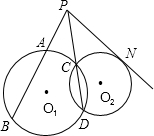如图，⊙O1与⊙O2相交于C、D两点，⊙O1的割线PAB与DC的延长线交于点P，PN与⊙O2相切于点N，若PB=10，AB=6，则PN=
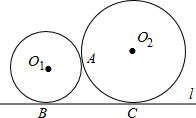已知：如图，⊙O1与⊙O2外切于A点，直线l与⊙O1、⊙O2分别切于B，C点，若⊙O1的半径r1=2cm，⊙O2的半径r2=3cm．求BC的长．
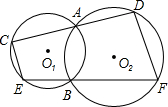已知如图：⊙O1与⊙O2相交于AB两点，过点A、B的直线分别与⊙O1交于C、E，与⊙O2交于D、F，连接CE、DF．