题目内容
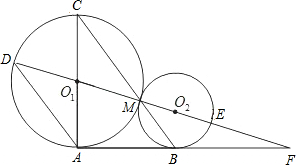 已知:如图,⊙O1与⊙O2外切于M点,AF是两圆的外公切线,A、B是切点,DF经过O1、O2,分别交⊙O1于D、⊙O2于E,AC是⊙O1的直径,BC经过M点,连接AD.
已知:如图,⊙O1与⊙O2外切于M点,AF是两圆的外公切线,A、B是切点,DF经过O1、O2,分别交⊙O1于D、⊙O2于E,AC是⊙O1的直径,BC经过M点,连接AD.(1)求证:AD∥BC;
(2)求证:MF2=AF•BF;
(3)如果⊙O1的直径长为8,tan∠ACB=
| 3 | 4 |
分析:(1)根据同弧的圆周角相等,先证∠ADM=∠ACB,再证△O1AD为等腰三角形,根据等量代换可证∠DAC=∠ACB,即可证得.
(2)要证结论,必先证△AMF∽△MBF,根据切线定理,即可证得∠ADO1=∠MAB,又在第1问的基础上进行等量代换,就可证得AAA.
(3)由切割线定理和勾股定理多次结合使用,即可求得.
(2)要证结论,必先证△AMF∽△MBF,根据切线定理,即可证得∠ADO1=∠MAB,又在第1问的基础上进行等量代换,就可证得AAA.
(3)由切割线定理和勾股定理多次结合使用,即可求得.
解答: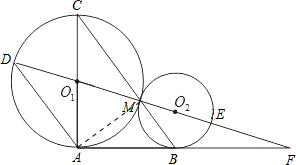 (1)证明:∵∠DO1A=∠CO1M,O1A=O1D=O1C=O1M
(1)证明:∵∠DO1A=∠CO1M,O1A=O1D=O1C=O1M
∴∠ADO1=∠O1MC=∠DAO1=∠O1CM(1分)
∴DA∥CM(2分)
(2)证明:连接AM,(3分)
∵∠BME=∠O1MC
又∵∠O1MC=∠ADO1∴∠BME=∠ADO1
又∵AB切⊙O1于A
∴∠ADO1=∠MAB
∴∠MAB=∠BME∠F=∠F
∴△MBF∽△AMF(4分)
∴
=
即:MF2=AF•BF(5分)
(3)解:在Rt△ACB中,
∵tan∠ACB=
=
又∵AC=8
∴AB=6(6分)
∵BC=
=10
∵AB2=BM•BC
∴62=BM×10
∴BM=3.6(7分)
又∵∠ACB=∠BME
∴tan∠BME=
=
∴BE=2.7(8分)
∴ME=
=4.5(9分).
 (1)证明:∵∠DO1A=∠CO1M,O1A=O1D=O1C=O1M
(1)证明:∵∠DO1A=∠CO1M,O1A=O1D=O1C=O1M∴∠ADO1=∠O1MC=∠DAO1=∠O1CM(1分)
∴DA∥CM(2分)
(2)证明:连接AM,(3分)
∵∠BME=∠O1MC
又∵∠O1MC=∠ADO1∴∠BME=∠ADO1
又∵AB切⊙O1于A
∴∠ADO1=∠MAB
∴∠MAB=∠BME∠F=∠F
∴△MBF∽△AMF(4分)
∴
| MF |
| AF |
| BF |
| MF |
即:MF2=AF•BF(5分)
(3)解:在Rt△ACB中,
∵tan∠ACB=
| AB |
| AC |
| 3 |
| 4 |
又∵AC=8
∴AB=6(6分)
∵BC=
| 62+82 |
∵AB2=BM•BC
∴62=BM×10
∴BM=3.6(7分)
又∵∠ACB=∠BME
∴tan∠BME=
| 3 |
| 4 |
| BE |
| BM |
∴BE=2.7(8分)
∴ME=
| 3.62+2.72 |
点评:切线长定理和切割线定理是中考的热点,掌握其用法,并与勾股定理和相似三角形综合应用,即可解答此类题.

练习册系列答案
相关题目
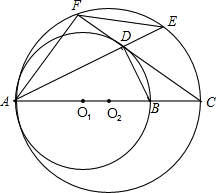 O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD.
O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD.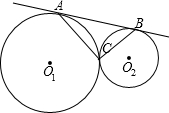 已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=
已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=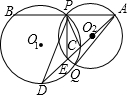 (1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且
(1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且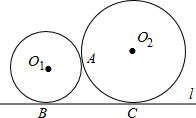 已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长.
已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长.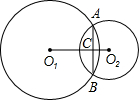 已知:如图,⊙O1与⊙O2相交于A、B,若两圆半径分别为12和5,O1O2=13,则AB=
已知:如图,⊙O1与⊙O2相交于A、B,若两圆半径分别为12和5,O1O2=13,则AB=