题目内容
12、已知：如图，⊙O1与⊙O2外切于点P，直线AB过点P交⊙O1于A，交⊙O2于B，点C、D分别为⊙O1、⊙O2上的点，且∠ACP=65°，则∠BDP=65
度．分析：过P做两圆的公切线MN，根据弦切角等于它所夹的弧所对的圆周角求解．
解答：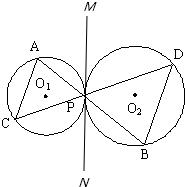
解：过P做两圆的公切线MN，
∴∠MPA=∠ACP，∠NPB=∠PDB，
∵∠MPA=∠NPB
∴∠BDP=∠ACP=65°．
解：过P做两圆的公切线MN，∴∠MPA=∠ACP，∠NPB=∠PDB，
∵∠MPA=∠NPB
∴∠BDP=∠ACP=65°．
点评：两圆相切，做公切线是常用的方法．用到的知识点为：弦切角等于它所夹的弧所对的圆周角．
练习册系列答案
相关题目
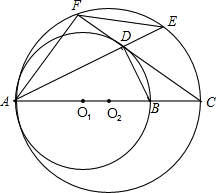O1于点D，AD的延长线交⊙O2于点E，连接AF、EF、BD．
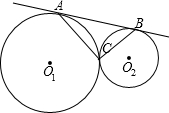已知：如图，⊙O1与⊙O2外切于C点，AB一条外公切线，A、B分别为切点，连接AC、BC．设⊙O1的半径为R，⊙O2的半径为r，若tan∠ABC=
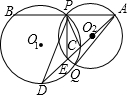（1998•南京）已知，如图，⊙O1与⊙O2相交，点P是其中一个交点，点A在⊙O2上，AP的延长线交⊙O1于点B，AO2的延长线交⊙O1于点C、D，交⊙O2于点E，连接PC、PE、PD，且
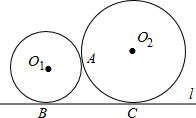已知：如图，⊙O1与⊙O2外切于A点，直线l与⊙O1、⊙O2分别切于B，C点，若⊙O1的半径r1=2cm，⊙O2的半径r2=3cm．求BC的长．
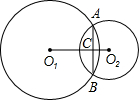已知：如图，⊙O1与⊙O2相交于A、B，若两圆半径分别为12和5，O1O2=13，则AB=