题目内容
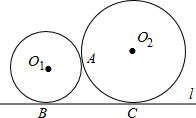 已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长.
已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长.分析:首先连接O1B,O2C,O1O2,过点O1作O1D⊥O2C于D,由直线l与⊙O1、⊙O2分别切于B,C点,可得四边形O1BCD是矩形,即可知CD=O1B=r1=2cm,BC=O1D,然后在Rt△O2DO1中,利用勾股定理即可求得O1D的长,即可得BC的长.
解答: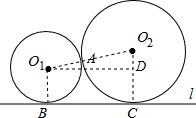 解:连接O1B,O2C,O1O2,过点O1作O1D⊥O2C于D,
解:连接O1B,O2C,O1O2,过点O1作O1D⊥O2C于D,
∵直线l与⊙O1、⊙O2分别切于B,C点,
∴O1B⊥BC,O2C⊥BC,
∴四边形O1BCD是矩形,
∴CD=O1B=r1=2cm,BC=O1D,
∴O2D=O2C-CD=3-2=1(cm),
∵,⊙O1与⊙O2外切于A点,
在Rt△O2DO1中,O2O1=r1+r2=2+3=5(cm),
∴O1D=2
(cm),
∴BC=2
cm.
 解:连接O1B,O2C,O1O2,过点O1作O1D⊥O2C于D,
解:连接O1B,O2C,O1O2,过点O1作O1D⊥O2C于D,∵直线l与⊙O1、⊙O2分别切于B,C点,
∴O1B⊥BC,O2C⊥BC,
∴四边形O1BCD是矩形,
∴CD=O1B=r1=2cm,BC=O1D,
∴O2D=O2C-CD=3-2=1(cm),
∵,⊙O1与⊙O2外切于A点,
在Rt△O2DO1中,O2O1=r1+r2=2+3=5(cm),
∴O1D=2
| 6 |
∴BC=2
| 6 |
点评:此题考查了相切两圆的性质、切线的性质、矩形的判定与性质以及勾股定理.此题难度适中,解题的关键是准确作出辅助线,掌握相切两圆的性质.

练习册系列答案
相关题目
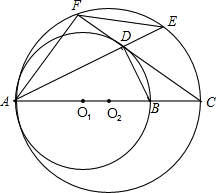 O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD.
O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD.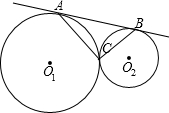 已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=
已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=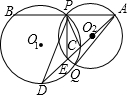 (1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且
(1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且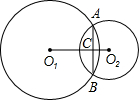 已知:如图,⊙O1与⊙O2相交于A、B,若两圆半径分别为12和5,O1O2=13,则AB=
已知:如图,⊙O1与⊙O2相交于A、B,若两圆半径分别为12和5,O1O2=13,则AB=