题目内容
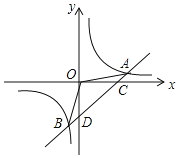
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3交x轴于点A(﹣1,0)和点B(3,0),与y轴交于点C,顶点是D,对称轴交x轴于点E.
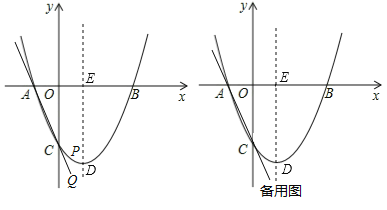
(1)求抛物线的解析式;
(2)点P是抛物线在第四象限内的一点,过点P作PQ∥y轴,交直线AC于点Q,设点P的横坐标是m.
①求线段PQ的长度n关于m的函数关系式;
②连接AP,CP,求当△ACP面积为![]() 时点P的坐标;
时点P的坐标;
(3)若点N是抛物线对称轴上一点,则抛物线上是否存在点M,使得以点B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出线段BN的长度;若不存在,请说明理由.
【答案】(1)y=x2﹣2x﹣3;(2)①n=m2+m;②P(![]() ,﹣
,﹣![]() );(3)存在,BN=2
);(3)存在,BN=2![]() 或2或2
或2或2![]()
【解析】
(1)抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),故﹣3a=﹣3,解得:a=1,即可求解;
(2)①AC的表达式为:y=﹣3x﹣3,则点Q(m,﹣3m﹣3),n=PQ=m2﹣2m﹣3+3m+3=m2+m;△ACP面积=![]() ×CH×(xP﹣xA)=
×CH×(xP﹣xA)=![]() m(m+1)=
m(m+1)=![]() ,即可求解;
,即可求解;
(3)分BC是边、BC是对角线两种情况,分别求解即可.
(1)抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),
故﹣3a=﹣3,解得:a=1,
故抛物线的表达式为:y=x2﹣2x﹣3;
(2)设点P(m,m2﹣2m﹣3),
①将点A、C的坐标代入一次函数表达式并解得:
直线AC的表达式为:y=﹣3x﹣3,则点Q(m,﹣3m﹣3),
n=PQ=m2﹣2m﹣3+3m+3=m2+m;
②连接AP交y轴于点H,

同理可得:直线AP的表达式为:y=(m﹣3)x+m﹣3,
则OH=3﹣m,则CH=m,
△ACP面积=![]() ×CH×(xP﹣xA)=
×CH×(xP﹣xA)=![]() m(m+1)=
m(m+1)=![]() ,
,
解得:m=![]() (不合题意的值已舍去),
(不合题意的值已舍去),
故点P(![]() ,﹣
,﹣![]() );
);
(3)点C(0,﹣3),点B(3,0),设点P(m,n),n=m2﹣2m﹣3,点N(1,s),
①当BC是边时,
点C向右平移3个单位向上平移3个单位得到B,
同样点M(N)向右平移3个单位向上平移3个单位得到N(M),
即1±3=m,s±3=n,
解得:m=4或﹣2,s=2或0,
故点N(1,2)或(1,0),则BN=2![]() 或2;
或2;
②当BC是对角线时,
由中点公式得:3=m+1,3=s+n,
解得:s=6,故点N(1,6),则BN=2![]() ,
,
综上,BN=2![]() 或2或2
或2或2![]() .
.