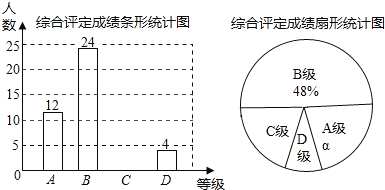
题目内容
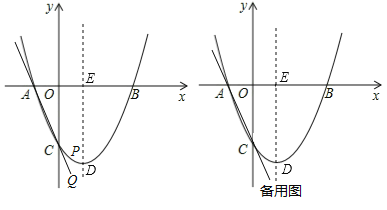
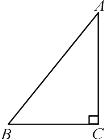
【题目】如图，在矩形ABCD中，已知
，
，点P是边BC上一动点（点P不与点B，C重合），连接AP，作点B关于直线AP的对称点M，连接MP，作
的角平分线交边CD于点N.则线段MN的最小值为_______________
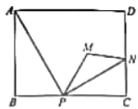
【答案】
【解析】
连接AM、AN，由翻折可得：
，然后根据
，故当A、M、N三点共线时，MN取得最小值，此时
，故当AN取得最小值时，MN最小，根据勾股定理可得：当DN最小时，AN最小,根据相似三角形的判定可得：
，列出比例式，设
，
，得出CN与x的二次函数的关系式，即可求出CN的最大值，从而求出DN的最小值，即可得出AN的最小值，从而求出线段MN的最小值.
解：连接AM、AN
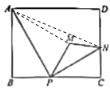
由翻折可得：
∴
当A、M、N三点共线时，MN取得最小值
即
∴当AN取得最小值时，MN最小
又∵
∴当DN最小时，AN最小
由翻折可得：
又∵PN平分
∴
∴
又∵
∴
∴
∴
∴
设，
∴
∴
∴ 当
时，
∴
∴
∴
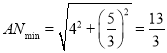
故答案为：.
练习册系列答案
相关题目
