题目内容
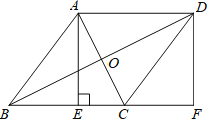
【题目】如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC至F,使CF=BE,连接DF.
(1)求证:四边形AEFD是矩形;
(2)若AC=10,∠ABC=60°,则矩形AEFD的面积是 .
【答案】(1)见解析;(2)50![]()
【解析】
(1)根据菱形的性质得到AD∥BC且AD=BC,等量代换得到BC=EF,推出四边形AEFD是平行四边形,根据矩形的判定定理即可得到结论;
(2)根据全等三角形的判定定理得到Rt△ABE≌Rt△DCF (HL),求得矩形AEFD的面积=菱形ABCD的面积,根据等腰三角形的性质得到结论.
(1)证明:∵四边形ABCD是菱形,
∴AD∥BC,AD=BC,
∵CF=BE,
∴BC=EF,
∴AD∥EF,AD=EF,
∴四边形AEFD是平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴平行四边形AEFD是矩形;
(2)∵AB=CD,BE=CF,∠AEB=∠DFC=90°,
∴Rt△ABE≌Rt△DCF (HL),
∴矩形AEFD的面积=菱形ABCD的面积,
∵∠ABC=60°,
∴△ABC是等边三角形,
∵AC=10,
∴AO=![]() AC=5,AB=10,BO=5
AC=5,AB=10,BO=5![]() ,
,
∴矩形AEFD的面积=菱形ABCD的面积=![]() ×10×10
×10×10![]() =50
=50![]() ,
,
故答案为:50![]() .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目