题目内容
【题目】已知∠MAN=135°,正方形ABCD绕点A旋转.
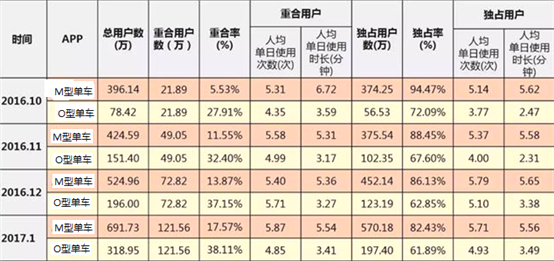
(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM,AN分别与正方形ABCD的边CB,CD的延长线交于点M,N,连接MN.
①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是 ;
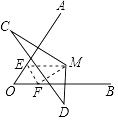
②如图2,若BM≠DN,请判断①中的数量关系是否仍成立?若成立,请给予证明;若不成立,请说明理由;
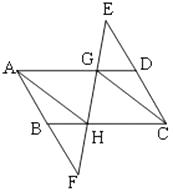
(2)如图3,当正方形ABCD旋转到∠MAN的内部(顶点A除外)时,AM,AN分别与直线BD交于点M,N,探究:以线段BM,MN,DN的长度为三边长的三角形是何种三角形,并说明理由.

【答案】(1)①MN=BM+DN;②成立;(2)直角三角形.
【解析】
试题分析:(1)①如图1,先证明△ADN≌△ABM,得到AN=AM,∠NAD=∠MAB,得到∠NAD=∠MAB=67.5°.作AE⊥MN于E,由等腰三角形三线合一的性质得出MN=2NE,∠NAE=67.5°.再证明△ADN≌△AEN,得出DN=EN,进而得到MN=BM+DN;
②如图2,先证明△ABM≌△ADP,得出AM=AP,∠1=∠2=∠3,再计算出∠PAN=135°.然后证明△ANM≌△ANP,得到MN=PN,进而得到MN=BM+DN;
(2)如图3,将△ABM绕点A逆时针旋转90°,得到△ADE,连结NE.由旋转的性质得到DE=BM,AE=AM,∠EAM=90°,∠NDE=90°. 先证明△AMN≌△AEN.得到MN=EN.由DN,DE,NE为直角三角形的三边,得到以线段BM,MN,DN的长度为三边长的三角形是直角三角形.
试题解析:(1)①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是MN=BM+DN.理由如下:
在△ADN与△ABM中,∵AD=AB,∠ADN=∠ABM,DN=BM,∴△ADN≌△ABM(SAS),∴AN=AM,∠NAD=∠MAB,∵∠MAN=135°,∠BAD=90°,∴∠NAD=∠MAB=![]() (360°﹣135°﹣90°)=67.5°,作AE⊥MN于E,则MN=2NE,∠NAE=
(360°﹣135°﹣90°)=67.5°,作AE⊥MN于E,则MN=2NE,∠NAE=![]() ∠MAN=67.5°.在△ADN与△AEN中,∵∠ADN=∠AEN,∠NAD=∠NAE,AN=AN,∴△ADN≌△AEN(AAS),∴DN=EN,∵BM=DN,MN=2EN,∴MN=BM+DN.故答案为:MN=BM+DN;
∠MAN=67.5°.在△ADN与△AEN中,∵∠ADN=∠AEN,∠NAD=∠NAE,AN=AN,∴△ADN≌△AEN(AAS),∴DN=EN,∵BM=DN,MN=2EN,∴MN=BM+DN.故答案为:MN=BM+DN;
②如图2,若BM≠DN,①中的数量关系仍成立.理由如下:
延长NC到点P,使DP=BM,连结AP.∵四边形ABCD是正方形,∴AB=AD,∠ABM=∠ADC=90°.在△ABM与△ADP中,∵AB=AD,∠ABM=∠ADP,BM=DP,∴△ABM≌△ADP(SAS),∴AM=AP,∠1=∠2=∠3,∵∠1+∠4=90°,∴∠3+∠4=90°,∵∠MAN=135°,∴∠PAN=360°﹣∠MAN﹣(∠3+∠4)=360°﹣135°﹣90°=135°.在△ANM与△ANP中,∵AM=AP,∠MAN=∠PAN,AN=AN,∴△ANM≌△ANP(SAS),∴MN=PN,∵PN=DP+DN=BM+DN,∴MN=BM+DN;
(2)以线段BM,MN,DN的长度为三边长的三角形是直角三角形.理由如下:
如图3,将△ABM绕点A逆时针旋转90°,得到△ADE,连结NE.由旋转的性质得:DE=BM,AE=AM,∠EAM=90°,∠NDE=90°. ∵∠MAN![]() 135°,∴∠EAN
135°,∴∠EAN![]() 360°
360°![]() ∠MAN
∠MAN![]() ∠EAM =135°,∴∠EAN =∠MAN.在△AMN与△AEN中,∵AM=AE,∠MAN=∠EAN,AN=AN,∴△AMN≌△AEN.∴MN=EN.∵DN,DE,NE为直角三角形的三边,∴以线段BM,MN,DN的长度为三边长的三角形是直角三角形.
∠EAM =135°,∴∠EAN =∠MAN.在△AMN与△AEN中,∵AM=AE,∠MAN=∠EAN,AN=AN,∴△AMN≌△AEN.∴MN=EN.∵DN,DE,NE为直角三角形的三边,∴以线段BM,MN,DN的长度为三边长的三角形是直角三角形.