Question

【题目】如图，抛物线y=ax2+bx+c（a≠0）与x轴相交于A（﹣1，0），B（3，0），与y轴交于点C（0，3）．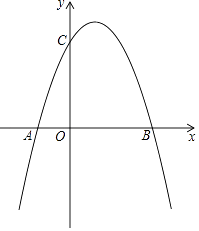

（1）求抛物线的解析式；
（2）连接BC，点P为抛物线上第一象限内一动点，当△BCP面积最大时，求点P的坐标；
（3）设点D是抛物线的对称轴上的一点，在抛物线上是否存在点Q，使以点B，C，D，Q为顶点的四边形为平行四边形？若存在，求出点Q的坐标；若不存在，说明理由．

Answer 1

【答案】
（1）

解：设抛物线解析式为y=a（x+1）（x﹣3），

把C（0，3）代入得a1（﹣3）=3，解得a=﹣1，

所以抛物线解析式为y=﹣（x+1）（x﹣3），即y=﹣x2+2x+3

（2）

解：设直线BC的解析式为y=kx+m，

把B（3，0），C（0，3）代入得 ，解得 ，

所以直线BC的解析式为y=﹣x+3，

作PM∥y轴交BC于M，如图1，

设P（x，﹣x2+2x+3），（0＜x＜3），则M（x，﹣x+3），

∴PM=﹣x2+2x+3﹣（﹣x+3）=﹣x2+3x，

∴S△PCB= 3PM=﹣ x2+ =﹣ （x﹣ ）2+ ，

当x= 时，△BCP的面积最大，此时P点坐标为（ ， ）

（3）

解：如图2，

抛物线的对称轴为直线x=1，

当四边形BCDQ为平行四边形，设D（1，a），则Q（4，a﹣3），

把Q（4，a﹣3）代入y=﹣x2+2x+3得a﹣3=﹣16+8+3，解得a=﹣2，

∴Q（4，﹣5）；

当四边形BCQD为平行四边形时，设D（1，a），则Q（﹣2，3+a），

把Q（﹣2，3+a）代入y=﹣x2+2x+3得3+a=﹣4﹣4+3，解得a=﹣8，

∴Q（﹣2，﹣5）；

当四边形BQCD为平行四边形时，设D（1，a），则Q（2，3﹣a），

把Q（2，3﹣a）代入y=﹣x2+2x+3得3﹣a=﹣4+4+3，解得a=0，

∴Q（2，3），

综上所述，满足条件的Q点坐标为（4，﹣5）或（﹣2，﹣5）或（2，3）．

【解析】（1）设交点式y=a（x+1）（x﹣3），然后把C点坐标代入求出a的值即可得到抛物线的解析式；（2）先利用待定系数法求出直线BC的解析式为y=﹣x+3，作PM∥y轴交BC于M，如图1，设P（x，﹣x2+2x+3），（0＜x＜3），则M（x，﹣x+3），利用三角形面积公式得到∴S△PCB= 3PM=﹣ x2+ ，然后根据二次函数的性质求解；（3）如图2，分类讨论：当四边形BCDQ为平行四边形，设D（1，a），利用点平移的坐标规律得到Q（4，a﹣3），然后把Q（4，a﹣3）代入y=﹣x2+2x+3中求出a即可得到Q点坐标；当四边形BCQD为平行四边形或四边形BQCD为平行四边形时，利用同样方法可求出对应Q点坐标．