题目内容
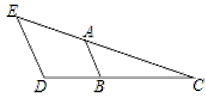
【题目】如图，∠E＝50°，∠BAC＝50°，∠D＝110°，求∠ABD的度数．
请完善解答过程，并在括号内填写相应的理论依据．
解：∵∠E＝50°，∠BAC＝50°，（已知）
∴∠E＝ （等量代换）
∴ ∥ ．（ ）
∴∠ABD+∠D＝180°．（ ）
∴∠D＝110°，（已知）
∴∠ABD＝70°．（等式的性质）
【答案】∠BAC AB DE 同位角相等，两直线平行 两直线平行，同旁内角互补
【解析】
先根据等量代换以及同位角相等，两直线平行判定AB∥DE，再根据两直线平行，同旁内角互补即可求得∠ABD的度数。
解：∵∠E＝50°，∠BAC＝50°，（已知）
∴∠E＝_∠BAC 等量代换）
∴AB∥DE．（ 同位角相等，两直线平行 ）
∴∠ABD+∠D＝180°．（ 两直线平行，同旁内角互补 ）
∴∠D＝110°，（已知）
∴∠ABD＝70°．（等式的性质）
故答案为：(1). ∠BAC (2). AB (3). DE (4). 同位角相等，两直线平行 (5). 两直线平行，同旁内角互补
练习册系列答案
相关题目
【题目】某市准备将一批帐篷和食品送往扶贫区．已知帐篷和食品共320件，且帐篷比食品多80件．
（1）直接写出帐篷有 件，食品有 件；
（2）现计划租用A、B两种货车共8辆，一次性将这批物资全部送到扶贫区，已知两种车可装帐篷和食品的件数以及每辆货车所需付运费情况如表，问：共有几种租车的方案？最少运费是多少？
帐篷（件） | 食品（件） | 每辆需付运费（元） | |
A种货车 | 40 | 10 | 780 |
B种货车 | 20 | 20 | 700 |
