题目内容
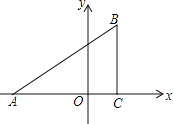
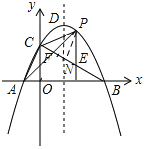
【题目】如图,抛物线y=﹣![]() (x+1)(x﹣9)与坐标轴交于A、B、C三点,D为顶点,连结AC,BC.点P是该抛物线在第一象限内上的一点.过点P作y轴的平行线交BC于点E,连结AP交BC于点F,则
(x+1)(x﹣9)与坐标轴交于A、B、C三点,D为顶点,连结AC,BC.点P是该抛物线在第一象限内上的一点.过点P作y轴的平行线交BC于点E,连结AP交BC于点F,则![]() 的最大值为_______.
的最大值为_______.
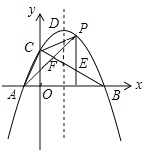
【答案】![]()
【解析】
根据抛物线的解析式求得A、B、C的坐标,进而求得AB、BC、AC的长,根据待定系数法求得直线BC的解析式,作PN⊥BC,垂足为N.先证明△PNE∽△BOC,由相似三角形的性质可知PN=![]() PE,然后再证明△PFN∽△AFC,由相似三角形的性质可得到PF:AF与m的函数关系式,从而可求得
PE,然后再证明△PFN∽△AFC,由相似三角形的性质可得到PF:AF与m的函数关系式,从而可求得![]() 的最大值.
的最大值.
∵抛物线y=﹣![]() (x+1)(x﹣9)与坐标轴交于A、B、C三点,
(x+1)(x﹣9)与坐标轴交于A、B、C三点,
∴A(﹣1,0),B(9,0),
令x=0,则y=3,
∴C(0,3),
∴BC![]() ,
,
设直线BC的解析式为y=kx+b.
∵将B、C的坐标代入得:![]() ,解得k=﹣
,解得k=﹣![]() ,b=3,
,b=3,
∴直线BC的解析式为y=﹣![]() x+3.
x+3.
设点P的横坐标为m,则纵坐标为﹣![]() (m+1)(m﹣9),点E(m,﹣
(m+1)(m﹣9),点E(m,﹣![]() m+3),
m+3),
∴PE=﹣![]() (m+1)(m﹣9)﹣(﹣
(m+1)(m﹣9)﹣(﹣![]() m+3)=﹣
m+3)=﹣![]() m2+3m.
m2+3m.
作PN⊥BC,垂足为N.
∵PE∥y轴,PN⊥BC,
∴∠PNE=∠COB=90°,∠PEN=∠BCO.
∴△PNE∽△BOC.
∴![]() =
=![]() =
=![]() =
=![]() .
.
∴PN=![]() PE=
PE=![]() (-
(-![]() m2+3m).
m2+3m).
∵AB2=(9+1)2=100,AC2=12+32=10,BC2=90,
∴AC2+BC2=AB2.
∴∠BCA=90°,
又∵∠PFN=∠CFA,
∴△PFN∽△AFC.
∴![]() =
=![]() =
=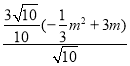 =﹣
=﹣![]() m2+
m2+![]() m=﹣
m=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() .
.
∵![]() ,
,
∴当m![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目