��Ŀ����
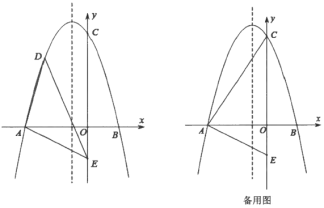
����Ŀ����ƽ��ֱ������ϵ�У�ֱ��y=x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��������y=a![]() +bx+c(a<0)������A��B��
+bx+c(a<0)������A��B��
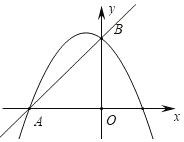
(1)��a��b����Ĺ�ϵʽ��c��ֵ��
(2)��x<0ʱ����y=a![]() +bx+c(a<0)�ĺ���ֵ��x�������������a��ȡֵ��Χ��
+bx+c(a<0)�ĺ���ֵ��x�������������a��ȡֵ��Χ��
(3)��ͼ����a=1ʱ�������������Ƿ���ڵ�P��ʹ��PAB�����Ϊ![]() ?�����ڣ�������������������е�P�����ꣻ�������ڣ���˵�����ɣ�
?�����ڣ�������������������е�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��b=3a+1��c=3����2��![]() ����3����P������Ϊ����
����3����P����������![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ��.
��.
��������
��1�������A��B�����꣬������⣻
��2����x��0ʱ����y=ax2+bx+c��a��0���ĺ���ֵ��x����������������Գ���![]() ����b=3a+1������
����b=3a+1������![]() ��������⣻
��������⣻
��3������P��ֱ��l��AB����PQ��y�ύBA�ڵ�Q����PH��AB�ڵ�H����S��PAB=![]() ����
����![]() =1��������⣮
=1��������⣮
�⣺��1��y=x+3����x=0����y=3����y=0����x=![]() ��
��
�ʵ�A��B������ֱ�Ϊ��-3��0������0��3������c=3��
��������ʽΪ��y=ax2+bx+3��
����A���������ʽ�������ã�b=3a+1��
��2����x��0ʱ����y=ax2+bx+c��a��0���ĺ���ֵ��x�����������
�����Գ���![]() ��
��
��![]() ��
��
��![]() ��
��
��ã�![]() ��
��
��a��ȡֵ��ΧΪ��![]() ��
��
��3����a=![]() ʱ��b=3a+1=
ʱ��b=3a+1=![]()
���κ�������ʽΪ��![]() ��
��
����P��ֱ��l��AB����PQ��y�ύBA�ڵ�Q����PH��AB�ڵ�H��
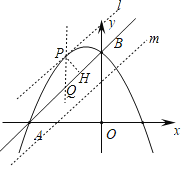
��OA=OB��
���BAO=��PQH=45�㣬
S��PAB=![]() ��AB��PH=
��AB��PH=![]() ��
��![]() ��PQ��
��PQ��![]() =
=![]() ��
��
��PQ=![]() =1��
=1��
��ֱ��AB�·���ֱ��m��ʹֱ��m��l��ֱ��AB�Ⱦ��룬
��ֱ��m���������������㣬�ֱ����AB��ɵ������ε����ҲΪ![]() ��
��
��![]() ��
��
���P��x��-x2-2x+3�������Q��x��x+3����
����-x2-2x+3-x-3=��1��
��ã�![]() ��
��![]() ��
��
���P����������![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ��.
��.

 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�